Asymmetric Contrarians in Opinion Dynamics
- PMID: 33285800
- PMCID: PMC7516446
- DOI: 10.3390/e22010025
Asymmetric Contrarians in Opinion Dynamics
Abstract
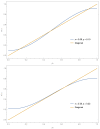
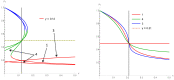
Asymmetry in contrarian behavior is investigated within the Galam model of opinion dynamics using update groups of size 3 with two competing opinions A and B. Denoting x and y the respective proportions of A and B contrarians, four schemes of implementations are studied. The first scheme activates contrarians after each series of updates with probabilities x and y for agents holding respectively opinion A and B. Second scheme activates contrarians within the update groups only against global majority with probability x when A is the majority and y when B is the majority. The third scheme considers in-group contrarians acting prior to the local majority update against both local majority and minority opinions. The last scheme activates in-group contrarians prior to the local majority update but only against the local majority. The main result is the loss of the fifty-fifty attractor produced by symmetric contrarians. Producing a bit less contrarians on its own side than the other side becomes the key to win a public debate, which in turn can guarantee an election victory. The associated phase diagram of opinion dynamics is found to exhibit a rich variety of counterintuitive results.
Keywords: local and global majority; opinion dynamics; sociophysics; tipping points.
Conflict of interest statement
The authors declare no conflict of interest.
Figures











Similar articles
-
Democratic Thwarting of Majority Rule in Opinion Dynamics: 1. Unavowed Prejudices Versus Contrarians.Entropy (Basel). 2025 Mar 14;27(3):306. doi: 10.3390/e27030306. Entropy (Basel). 2025. PMID: 40149230 Free PMC article.
-
Chaotic, staggered, and polarized dynamics in opinion forming: The contrarian effect.Phys Rev E Stat Nonlin Soft Matter Phys. 2006 Jun;73(6 Pt 2):066118. doi: 10.1103/PhysRevE.73.066118. Epub 2006 Jun 14. Phys Rev E Stat Nonlin Soft Matter Phys. 2006. PMID: 16906925
-
Voter models with contrarian agents.Phys Rev E Stat Nonlin Soft Matter Phys. 2013 Nov;88(5):052803. doi: 10.1103/PhysRevE.88.052803. Epub 2013 Nov 4. Phys Rev E Stat Nonlin Soft Matter Phys. 2013. PMID: 24329314
-
Majority rules: how good are we at aggregating convergent opinions?Evol Hum Sci. 2019 May 31;1:e6. doi: 10.1017/ehs.2019.6. eCollection 2019. Evol Hum Sci. 2019. PMID: 37588400 Free PMC article. Review.
-
Cephalostatin analogues--synthesis and biological activity.Fortschr Chem Org Naturst. 2004;87:1-80. doi: 10.1007/978-3-7091-0581-8_1. Fortschr Chem Org Naturst. 2004. PMID: 15079895 Review.
Cited by
-
Vanishing Opinions in Latané Model of Opinion Formation.Entropy (Basel). 2022 Dec 28;25(1):58. doi: 10.3390/e25010058. Entropy (Basel). 2022. PMID: 36673198 Free PMC article.
References
-
- Noorazar H., Vixie K.R., Talebanpour A., Hu Y. From classical to modern opinion dynamics. arXiv. 20191909.12089v2
-
- Calvão A.M., Ramos M., Anteneodo C. Role of the plurality rule in multiple choices. J. Stat. Mech. 2016;2016:023405. doi: 10.1088/1742-5468/2016/02/023405. - DOI
-
- Ajmone Marsan G., Bellomo N., Gibelli L. Stochastic evolutionary differential games toward a systems theory of behavioral social dynamics. Math. Models Methods Appl. Sci. 2016;26:1051–1093. doi: 10.1142/S0218202516500251. - DOI
-
- Carbone G., Giannoccaro I. Model of human collective decision-making in complex environments. Eur. Phys. J. 2015;88:339. doi: 10.1140/epjb/e2015-60609-0. - DOI
LinkOut - more resources
Full Text Sources
Miscellaneous

