Incorporating Cellular Stochasticity in Solid-Fluid Mixture Biofilm Models

Abstract

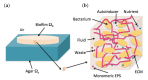
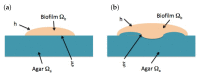
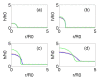
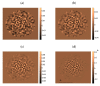
The dynamics of cellular aggregates is driven by the interplay of mechanochemical processes and cellular activity. Although deterministic models may capture mechanical features, local chemical fluctuations trigger random cell responses, which determine the overall evolution. Incorporating stochastic cellular behavior in macroscopic models of biological media is a challenging task. Herein, we propose hybrid models for bacterial biofilm growth, which couple a two phase solid/fluid mixture description of mechanical and chemical fields with a dynamic energy budget-based cellular automata treatment of bacterial activity. Thin film and plate approximations for the relevant interfaces allow us to obtain numerical solutions exhibiting behaviors observed in experiments, such as accelerated spread due to water intake from the environment, wrinkle formation, undulated contour development, and the appearance of inhomogeneous distributions of differentiated bacteria performing varied tasks.

Keywords: Von Karman plate; biofilm; cell differentiation; cellular activity; dynamic energy budget; osmotic spread; solid–fluid mixture; thin film; wrinkle formation.

Figure 1

Virtual visualization of a biofilm spreading on agar.

Figure 2

Schematic structure of a biofilm: (a) View of the macroscopic configuration: a biofilm on an agar–air interface. (b) Microstructure formed by biomass (polymeric mesh and cells) and fluid containing dissolved substances (nutrients, waste, and autoinducers).

Figure 3

Schematic representation of a biofilm slice, with moving air–biofilm interface h and agar–biofilm interface $\xi$. (a) Initial stages: $\xi$ is flat. (b) Later evolution: $\xi$ deviates out of a plane.

Figure 4

Biofilm height at dimensionless times 0 (a), 1 (b), 6 (c), and 7 (d) for $K={10}^{-5}$ and $h_{inf}={10}^{-3}.$ The dotted red line and the solid blue line depict the numerical solutions of (20) and (19), respectively, with R given by (21) and keeping the same data. We can observe the transition from an initial stage in which increase in biofilm height dominates to a stage with faster horizontal spread. The green line is a reference self-similar approximation.

Figure 5

Wrinkle formation and coarsening in a growing film with residual stresses computed from analytical formulas for the pressures. As the approximation breaks down, the height of the central wrinkles increases much faster than the height of the outer ones, which blur in comparison. Snapshots taken at times (a) $1.8/g$, (b) $2/g$, (c) $2.2/g$, and (d) $2.4/g$, starting from a randomly perturbed biofilm of radius $R_0={10}^{-3}$ m and height $h_0={10}^{-4}$ m. The radius does not vary significantly during this time, whereas the height becomes of the order of the radius at the end. Parameter values: $1/g=2.3$ hours, ${\mu }_f=8.9\times {10}^{-4}$ Pa·s at 25^o, ${\xi }_{\infty }=70$ nm, ${\varphi }_{\infty }=0.2$, $h_a=100h_0$, $\Pi =30$ Pa (taken from [11]), $E=25$ kPa (taken from [12]), $\nu =0.4$, ${\mu }_s=8.92$ kPa, ${\nu }_a=0.45$, ${\eta }_a=1$ kPa·s, ${\mu }_a=0$, $h_{inf}=h_0/10$.

Figure 6

Layered distribution of dead, active, and inert cells, as illustrated by slices of a growing biofilm. Dead cells appear at the bottom of three peaks present in the initial biofilm seed.

Figure 7

Top view of the evolution of a biofilm seed formed by two layers of cells with a diameter of 40 cells, depicted at steps: (a) 45; (b) 90; (c) 135; (d) 180; (e) 225; (f) 270. Darkest colors correspond to layers of increasing height up to 10 cells. Contour undulations develop as the biofilm spreads.

Figure 8

Snapshots of wrinkle formation, coarsening and branching as a circular biofilm expands following (27) and (28) and using an empirical fit to the residual stresses generated by cellular processes. The biofilm has Poisson ratio $\nu =0.5$ and Young modulus $E=25$ kPa. The Poisson ratio and rubbery modulus of the substratum are ${\nu }_v=0.45$, ${\mu }_v=0,$ and $\gamma =16$. (a) $26\frac{T}{\tau }$ s; (b) $260\frac{T}{\tau }$ s; (c) $520\frac{T}{\tau }$ s; (d) $780\frac{T}{\tau }$ s; (e) $1040\frac{T}{\tau }$ s; (f) $1300\frac{T}{\tau }$ s; (g) $1560\frac{T}{\tau }$ s; (h) $1820\frac{T}{\tau }$ s;

Figure 9

Effect of the presence of dead regions in liquid transport. Initial volume fractions: (a) water, (b) dead cells, and (c) alive cells. Snapshot showing dead cell reabsorption and water accumulation in the originally dead regions at a later time: volume fractions of (d) water, (e) dead cells, and (f) alive cells.