Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Feb 13;22(2):213.
doi: 10.3390/e22020213.

Variational Information Bottleneck for Unsupervised Clustering: Deep Gaussian Mixture Embedding

Yiğit Uğur  1   2 , George Arvanitakis  2 , Abdellatif Zaidi  1
Affiliations

Variational Information Bottleneck for Unsupervised Clustering: Deep Gaussian Mixture Embedding

Yiğit Uğur et al. Entropy (Basel). .

Abstract

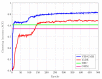
In this paper, we develop an unsupervised generative clustering framework that combines the variational information bottleneck and the Gaussian mixture model. Specifically, in our approach, we use the variational information bottleneck method and model the latent space as a mixture of Gaussians. We derive a bound on the cost function of our model that generalizes the Evidence Lower Bound (ELBO) and provide a variational inference type algorithm that allows computing it. In the algorithm, the coders' mappings are parametrized using neural networks, and the bound is approximated by Markov sampling and optimized with stochastic gradient descent. Numerical results on real datasets are provided to support the efficiency of our method.

Keywords: Gaussian mixture model; clustering; information bottleneck; unsupervised learning.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Variational Information Bottleneck with Gaussian mixtures.
Figure 2
Figure 2
Inference network.
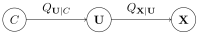
Figure 3
Figure 3
Generative network.
Figure 4
Figure 4
Accuracy vs. the number of epochs for the STL-10dataset.
Figure 5
Figure 5
Information plane for the STL-10 dataset.
Figure 6
Figure 6
Visualization of the latent space before training; and after 1, 5, and 500 epochs.
See this image and copyright information in PMC

References

    1. Sculley D. Web-scale K-means clustering; Proceedings of the 19th International Conference on World Wide Web; Raleigh, NC, USA. 26–30 April 2010; pp. 1177–1178.
    1. Huang Z. Extensions to the k-means algorithm for clustering large datasets with categorical values. Data Min. Knowl. Disc. 1998;2:283–304. doi: 10.1023/A:1009769707641. - DOI
    1. Hartigan J.A., Wong M.A. Algorithm AS 136: A K-means clustering algorithm. J. R. Stat. Soc. 1979;28:100–108. doi: 10.2307/2346830. - DOI
    1. Dempster A.P., Laird N.M., Rubin D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977;39:1–38.
    1. Ding C., He X. K-means clustering via principal component analysis; Proceedings of the 21st International Conference on Machine Learning; Banff, AB, Canada. 4–8 July 2004.

LinkOut - more resources