Thermomass Theory in the Framework of GENERIC
- PMID: 33286001
- PMCID: PMC7516658
- DOI: 10.3390/e22020227
Thermomass Theory in the Framework of GENERIC
Abstract
Thermomass theory was developed to deal with the non-Fourier heat conduction phenomena involving the influence of heat inertia. However, its structure, derived from an analogy to fluid mechanics, requires further mathematical verification. In this paper, General Equation for Non-Equilibrium Reversible-Irreversible Coupling (GENERIC) framework, which is a geometrical and mathematical structure in nonequilibrium thermodynamics, was employed to verify the thermomass theory. At first, the thermomass theory was introduced briefly; then, the GENERIC framework was applied in the thermomass gas system with state variables, thermomass gas density ρh and thermomass momentum mh, and the time evolution equations obtained from GENERIC framework were compared with those in thermomass theory. It was demonstrated that the equations generated by GENERIC theory were the same as the continuity and momentum equations in thermomass theory with proper potentials and eta-function. Thermomass theory gives a physical interpretation to the GENERIC theory in non-Fourier heat conduction phenomena. By combining these two theories, it was found that the Hamiltonian energy in reversible process and the dissipation potential in irreversible process could be unified into one formulation, i.e., the thermomass energy. Furthermore, via the framework of GENERIC, thermomass theory could be extended to involve more state variables, such as internal source term and distortion matrix term. Numerical simulations investigated the influences of the convective term and distortion matrix term in the equations. It was found that the convective term changed the shape of thermal energy distribution and enhanced the spreading behaviors of thermal energy. The distortion matrix implies the elasticity and viscosity of the thermomass gas.
Keywords: GENERIC; hyperbolic heat conduction; thermomass; thermomass energy.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
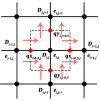



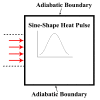
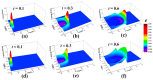
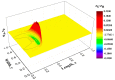

References
-
- Ackerman C.C., Bertman B., Fairbank H.A., Guyer R.A. Second Sound in Solid Helium. Phys. Rev. Lett. 1966;16:789–791. doi: 10.1103/PhysRevLett.16.789. - DOI
-
- McNelly T.F., Rogers S.J., Channin D.J., Rollefson R.J., Goubau W.M., Schmidt G.E., Krumhansl J.A., Pohl R.O. Heat pulses in NaF: Onset of second sound. Phys. Rev. Lett. 1970;24:100. doi: 10.1103/PhysRevLett.24.100. - DOI
-
- Jackson H.E., Walker C.T., McNelly T.F. Second sound in NaF. Phys. Rev. Lett. 1970;25:26. doi: 10.1103/PhysRevLett.25.26. - DOI
-
- Narayanamurti V., Dynes R. Observation of second sound in bismuth. Phys. Rev. Lett. 1972;28:1461. doi: 10.1103/PhysRevLett.28.1461. - DOI
-
- Pohl D.W., Irniger V. Observation of Second Sound in NaF by Means of Light Scattering. Phys. Rev. Lett. 1976;36:480–483. doi: 10.1103/PhysRevLett.36.480. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

