Robust Regression with Density Power Divergence: Theory, Comparisons, and Data Analysis

Abstract

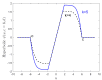
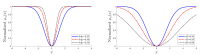
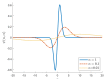
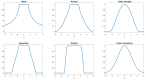
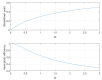
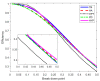
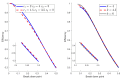
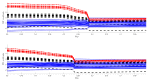
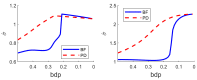
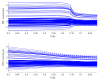
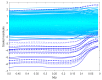
Minimum density power divergence estimation provides a general framework for robust statistics, depending on a parameter α , which determines the robustness properties of the method. The usual estimation method is numerical minimization of the power divergence. The paper considers the special case of linear regression. We developed an alternative estimation procedure using the methods of S-estimation. The rho function so obtained is proportional to one minus a suitably scaled normal density raised to the power α . We used the theory of S-estimation to determine the asymptotic efficiency and breakdown point for this new form of S-estimation. Two sets of comparisons were made. In one, S power divergence is compared with other S-estimators using four distinct rho functions. Plots of efficiency against breakdown point show that the properties of S power divergence are close to those of Tukey's biweight. The second set of comparisons is between S power divergence estimation and numerical minimization. Monitoring these two procedures in terms of breakdown point shows that the numerical minimization yields a procedure with larger robust residuals and a lower empirical breakdown point, thus providing an estimate of α leading to more efficient parameter estimates.

Keywords: S-estimation; Tukey’s biweight; estimation of α; monitoring; numerical minimization.

Figure A1

Hyperbolic tangent $\psi$ function for two values of the parameter k.

Figure 1

Dependence of ${\rho }_{\alpha }\left(x\right)$ on $\alpha$, for frequently used values of robustness properties in Table 1. Left-hand panel, three values of breakdown point (bdp); right-hand panel, three values of eff.

Figure 2

S power divergence; $\psi$ function, proportional to the influence function.

Figure 3

The weight function $\psi \left(x\right)/x$ for six S-estimators.

Figure 4

S power divergence: breakdown point and efficiency as functions of $\alpha$.

Figure 5

Breakdown point and efficiency as parameters vary for five rho functions: TB = Tukey biweight; HA = Hampel; OPT = optimal; PD = power divergence and HYP = hyperbolic. The inset is a zoom of the main figure for high breakdown point.

Figure 6

Breakdown point and efficiency as parameters vary for the Hampel and hyperbolic rho functions.

Figure 7

Regression data: residuals as bdp decreases. Upper panel, Brute Force (BF)-estimation, lower panel S-estimation.

Figure 8

Comparison of estimates of $\sigma$ as bdp decreases. Left-hand panel, regression data: right-hand panel, data with moderate outliers.

Figure 9

Data with moderate outliers: residuals as bdp decreases. Upper panel, BF-estimation; lower panel S-estimation.

Figure 10

Loyalty card data: residuals for BF-estimation as bdp decreases.