Taylor's Law in Innovation Processes
- PMID: 33286342
- PMCID: PMC7517092
- DOI: 10.3390/e22050573
Taylor's Law in Innovation Processes
Abstract
Taylor's law quantifies the scaling properties of the fluctuations of the number of innovations occurring in open systems. Urn-based modeling schemes have already proven to be effective in modeling this complex behaviour. Here, we present analytical estimations of Taylor's law exponents in such models, by leveraging on their representation in terms of triangular urn models. We also highlight the correspondence of these models with Poisson-Dirichlet processes and demonstrate how a non-trivial Taylor's law exponent is a kind of universal feature in systems related to human activities. We base this result on the analysis of four collections of data generated by human activity: (i) written language (from a Gutenberg corpus); (ii) an online music website (Last.fm); (iii) Twitter hashtags; (iv) an online collaborative tagging system (Del.icio.us). While Taylor's law observed in the last two datasets agrees with the plain model predictions, we need to introduce a generalization to fully characterize the behaviour of the first two datasets, where temporal correlations are possibly more relevant. We suggest that Taylor's law is a fundamental complement to Zipf's and Heaps' laws in unveiling the complex dynamical processes underlying the evolution of systems featuring innovation.
Keywords: Poisson–Dirichlet process; Pólya’s urn; Taylor’s law; adjacent possible; innovation dynamics; triangular urn schemes.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


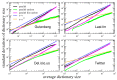

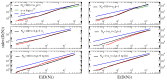
References
-
- Zipf G.K. Relative Frequency as a Determinant of Phonetic Change. Harv. Stud. Class. Philol. 1929;40:1–95. doi: 10.2307/310585. - DOI
-
- Zipf G.K. The Psychobiology of Language. Houghton-Mifflin; New York, NY, USA: 1935.
-
- Zipf G.K. Human Behavior and the Principle of Least Effort. Addison-Wesley; Reading MA, USA: 1949.
-
- Herdan G. Type-Token Mathematics: A Textbook of Mathematical Linguistics. Mouton en Company; Berlin, Germany: 1960. (Janua linguarum. series maior. no. 4).
-
- Heaps H.S. Information Retrieval-Computational and Theoretical Aspects. Academic Press; Cambridge, MA, USA: 1978.
LinkOut - more resources
Full Text Sources

