A Review of Methods for Estimating Algorithmic Complexity: Options, Challenges, and New Directions

Abstract

Some established and also novel techniques in the field of applications of algorithmic (Kolmogorov) complexity currently co-exist for the first time and are here reviewed, ranging from dominant ones such as statistical lossless compression to newer approaches that advance, complement and also pose new challenges and may exhibit their own limitations. Evidence suggesting that these different methods complement each other for different regimes is presented and despite their many challenges, some of these methods can be better motivated by and better grounded in the principles of algorithmic information theory. It will be explained how different approaches to algorithmic complexity can explore the relaxation of different necessary and sufficient conditions in their pursuit of numerical applicability, with some of these approaches entailing greater risks than others in exchange for greater relevance. We conclude with a discussion of possible directions that may or should be taken into consideration to advance the field and encourage methodological innovation, but more importantly, to contribute to scientific discovery. This paper also serves as a rebuttal of claims made in a previously published minireview by another author, and offers an alternative account.

Keywords: Kolmogorov complexity; Lempel–Ziv–Welch (LZW); Shannon entropy; algorithmic complexity; block decomposition method; causality v correlation; coding theorem method; lossless compression; practical feasibility; rebuttal to Paul Vitányi’s review.

Figure 1

(A) An observer trying to characterise an observed stream of data (s) of unknown source (in this case, the sequence of natural numbers in decimal or binary that the observer may not recognise) has currently two options: (B) the statistical compression approach (green arrow) represented by run-length encoding (RLE), producing a rather cryptic and even longer description than the original observation with no clear correspondence between possible ground and represented states; or alternatively, (C) an approach that takes on the challenge as in an inverse problem represented by the Coding theorem method (CTM) (green arrow) that allows finding the set of small computer programs according to some 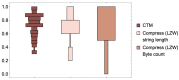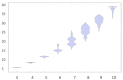reference machine up to a certain size that match their output to the original observation thereby potentially reverse engineering of the generating mechanism that may have recursively produced the sequence in the first place. (D) Such an approach allows a state space description represented by a generative rule or transition table and a state diagram whose elements may correspond (or not) to a physical unfolding phenomenon against which it can be tested (notice that the binary to decimal Turing machines (TM) is also of a finite, small size and is only an intermediate step to arrive at s, but can be one of the engines behind it; here, for illustration purposes, only the TM binary counter is shown as an example).

Figure 2

Test for model internal consistency and optimality. The number of rules used in the transition table for the first and shortest Turing machine producing a string following the enumeration is in agreement with the estimation arrived at by CTM after application of the Coding theorem under the assumptions of optimality. Adapted from [53].

Figure 3

Agreement in shape and ranking of empirical distributions produced by three completely different models of computation: Turing machines (TM), cellular automata (CA), and post tag systems (TS), all three universal Turing models of computation for the same set of strings of length $k=5$ and $k=6$ for purposes of illustration only (comparison was made across all string lengths up to around 20, which already included a large set of $2^{20}$ strings).

Figure 4

This is the first ever empirical probability distribution produced by all the 15,059,072 Turing machines with three states and two symbols as reported in [29]. CTM has produced several comprehensive large tables for all binary (and also non-binary [60]) Turing machines with up to four and five states (and currently for six states) and is currently also computing for six states on one of the largest super computers available. The distributions (this and the much larger ones that followed) have shed light on many matters, from long standing challenges (the short string regime left uncovered by statistical compression), to the impact of the change of choice of computational power on empirical output distributions, to applications tested in the field that require high sensitivity (such as perturbation analysis [39,40]).

Figure 5

(A) Unlike compression, which behaves just like the Shannon entropy, CTM approximates the long-tail shape of the universal distribution, better conforming with the theory under strong assumptions of optimality. We call these causal gaps (A,B) because they are precisely the cases in which strings can be explained by a computer program of length far removed from the greatest program length of the most algorithmically random strings according to our (universal) computational model. (C) Divergence of CTM from entropy (and therefore LZW). Adapted from [38].

Figure 6

Density histograms showing how poorly lossless compression performs on short strings (just 12 bits in length), collapsing all values into two to four clusters, while CTM produces a finer-grained classification of 36 groups of strings. CTM (and BDM) can be calculated using the Online Algorithmic Complexity Calculator (https://complexitycalculator.com/).

Figure 7

Each “drop-like” distribution represents the set of strings that are minimally produced with the same number of instructions (Y axis) for all machines with up to four states for which there can be up to $2(n+1)=10$ transition rules. The more instructions needed to produce the strings, the more complex they are shown to be according to CTM (Y axis), after applying a Coding theorem-like equation to the empirical probability values for each string. The results conform with the theoretical expectation: the greater CTM, the greater the number of instructions used by the shortest Turing machine according to the enumeration, and vice versa. Adapted from [53].