Information Transfer in Linear Multivariate Processes Assessed through Penalized Regression Techniques: Validation and Application to Physiological Networks

Abstract

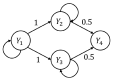
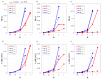
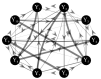
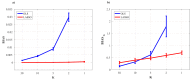
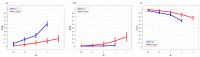
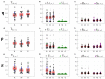
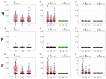
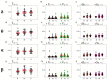
The framework of information dynamics allows the dissection of the information processed in a network of multiple interacting dynamical systems into meaningful elements of computation that quantify the information generated in a target system, stored in it, transferred to it from one or more source systems, and modified in a synergistic or redundant way. The concepts of information transfer and modification have been recently formulated in the context of linear parametric modeling of vector stochastic processes, linking them to the notion of Granger causality and providing efficient tools for their computation based on the state-space (SS) representation of vector autoregressive (VAR) models. Despite their high computational reliability these tools still suffer from estimation problems which emerge, in the case of low ratio between data points available and the number of time series, when VAR identification is performed via the standard ordinary least squares (OLS). In this work we propose to replace the OLS with penalized regression performed through the Least Absolute Shrinkage and Selection Operator (LASSO), prior to computation of the measures of information transfer and information modification. First, simulating networks of several coupled Gaussian systems with complex interactions, we show that the LASSO regression allows, also in conditions of data paucity, to accurately reconstruct both the underlying network topology and the expected patterns of information transfer. Then we apply the proposed VAR-SS-LASSO approach to a challenging application context, i.e., the study of the physiological network of brain and peripheral interactions probed in humans under different conditions of rest and mental stress. Our results, which document the possibility to extract physiologically plausible patterns of interaction between the cardiovascular, respiratory and brain wave amplitudes, open the way to the use of our new analysis tools to explore the emerging field of Network Physiology in several practical applications.

Keywords: State–space models; conditional transfer entropy; entropy; information dynamics; linear prediction; multivariate time series analysis; network physiology; partial information decomposition; penalized regression techniques; vector autoregressive model.

Figure 1

Graphical representation of the four-variate VAR (Vector Autoregressive) process realized in the first simulation according to Equation (17). Network nodes represent the four simulated processes, and arrows represent the imposed causal interactions (self-loops depict influences from the past to the present sample of a process).

Figure 2

Accuracy of PID (Partial Information Decomposition) measures computed for the VAR processes of Simulation I when $Y_4$ is taken as the target process. Panels report the bias (a–c) and the variance (d–f) relevant the computation of the TE (Transfer Entropy) from $Y_2$ to $Y_4$ and from $Y_3$ to $Y_4$ (a,d), the unique TE from $Y_2$ to $Y_4$ and from $Y_3$ to $Y_4$ (b,e) and the redundant and synergistic TE from $Y_2$ and $Y_3$ to $Y_4$ (c,f).

Figure 3

Accuracy of PID measures computed for the VAR processes of Simulation I when $Y_1$ is taken as the target process. Panels report the bias (a–c) and the variance (d–f) relevant the computation of the TE from $Y_2$ to $Y_1$ and from $Y_3$ to $Y_1$ (a,d), the unique TE from $Y_2$ to $Y_1$ and from $Y_3$ to $Y_1$ (b,e) and the redundant and synergistic TE from $Y_2$ and $Y_3$ to $Y_1$ (c,f).

Figure 4

Graphical representation for one of the ground-truth networks of Simulation II. Arrows represent the existence of a link, randomly assigned, between two nodes in the network. The thickness of the arrows is proportional to the strength of the connection, with a maximum value for the cTE equal to 0.15. The number of connections for each network is set to 45 out of 90.

Figure 5

Distribution of the bias parameters computed for the null links ($BIAS$, a) and for the non-null links ($BIA{S}_N$, b) considering the interaction factor K × TYPE, expressed as mean value and 95% confidence interval of the parameter computed across 100 realizations of simulation II for OLS (blue line) and LASSO (red line) for different values of K.

Figure 6

Distributions of $FNR$ (a), $FPR$ (b) and $ACC$ (c) parameters considering the interaction factor K x TYPE, expressed as mean value and 95% confidence interval of the parameter computed across 100 realizations of simulation II for OLS (blue line) and LASSO (red line) for different values of K.

Figure 7

Partial Information Decomposition of brain–body interactions directed to the body nodes of the physiological network, assessed using OLS VAR identification. Box plots report the distributions across subjects (median: red lines; interquartile range: box; 10^th–90^th percentiles: blue lines) as well as the individual values (circles or triangles) of the PID measures (a,d,g: joint information transfer; b,e,h: unique information transfer; c,f,i: synergistic and redundant transfer) computed at rest (R), during mental stress (M) and during serious game (G) considering the RR interval ($\eta$), the respiratory amplitude ($\rho$), or the pulse arrival time ($\pi$) as the target process j, and the body and brain sub-networks as source processes i and k. Statistically significant differences between pairs of distributions are marked with * (R vs. M), with # (R vs. G), with § (R vs. R), with ∼ (M vs. M) and with ∘ (G vs. G).

Figure 8

Partial Information Decomposition of brain–body interactions directed to the body nodes of the physiological network, assessed using LASSO-VAR identification. Box plots report the distributions across subjects (median: red lines; interquartile range: box; 10^th–90^th percentiles: blue lines) as well as the individual values (circles or triangles) of the PID measures (a,d,g: joint information transfer; b,e,h: unique information transfer; c,f,i: synergistic and redundant transfer) computed at rest (R), during mental stress (M) and during serious game (G) considering the RR interval ($\eta$), the respiratory amplitude ($\rho$), or the pulse arrival time ($\pi$) as the target process j, and the body and brain sub-networks as source processes i and k. Statistically significant differences between pairs of distributions are marked with * (R vs. M), with # (R vs. G), with § (R vs. R), with ∼ (M vs. M) and with ∘ (G vs. G).

Figure 9

Partial Information Decomposition of brain–body interactions directed to the brain nodes of the physiological network, assessed using OLS VAR identification. Box plots report the distributions across subjects (median: red lines; interquartile range: box; 10^th–90^th percentiles: blue lines) as well as the individual values (circles or triangles) of the PID measures (a,d,g,j: joint information transfer; b,e,h,k: unique information transfer; c,f,i,l: synergistic and redundant transfer) computed at rest (R), during mental stress (M) and during serious game (G) considering the $\delta$, $\theta$, $\alpha$, or $\beta$ brain wave amplitude as the target process j, and the body and brain sub-networks as source processes i and k. Statistically significant differences between pairs of distributions are marked with * (R vs. M), with # (R vs. G), with § (R vs. R), with ∼ (M vs. M) and with ∘ (G vs. G).

Figure 10

Partial Information Decomposition of brain–body interactions directed to the brain nodes of the physiological network, assessed using LASSO-VAR identification. Box plots report the distributions across subjects (median: red lines; interquartile range: box; 10^th–90^th percentiles: blue lines) as well as the individual values (circles or triangles) of the PID measures (a,d,g,j: joint information transfer; b,e,h,k: unique information transfer; c,f,i,l: synergistic and redundant transfer) computed at rest (R), during mental stress (M) and during serious game (G) considering the $\delta$, $\theta$, $\alpha$, or $\beta$ brain wave amplitude as the target process j, and the body and brain sub-networks as source processes i and k. Statistically significant differences between pairs of distributions are marked with * (R vs. M), with # (R vs. G), with § (R vs. R), with ∼ (M vs. M) and with ∘ (G vs. G).

Figure 11

Topological structure for the networks of physiological interactions reconstructed during the three analyzes physiological states. Graphs depict significant directed interactions within the brain (yellow arrows) and body (red arrows) sub-networks as well as interactions between brain and body (blue arrows). Directed interactions were assessed counting the number of subjects for which the conditional transfer entropy ($T_{i\to j|s}$) was detected as statistically significant using OLS (a–c) or LASSO (d–f) to perform VAR model identification. The arrow thickness is proportional to the number of subjects (n) for which the link is detected as statistically significant.

Figure 12

Bar plots reporting the in-strength index extracted from the cTE networks of Figure 11 by considering as link weights the percentage of subjects showing a brain-to-body connection (a) or a body-to-brain connection (b), computed at rest (R), during mental stress (M) and during serious game (G) for the two VAR identification methods. Please note that the in-strength computed along the direction from body to brain using LASSO is null in all conditions.

Figure 13

In-strength index computed for each node of the physiological network. Box plots report the distributions across subjects (median: red lines; interquartile range: box; 10^th–90^th percentiles: blue bars) as well as the individual values (circles) of the in-strength index (a-g) OLS, h-p LASSO) computed at rest (R), during mental stress (M) and during serious game (G) for each node ($\eta$,$\rho$,$\pi$,$\delta$,$\theta$,$\alpha$,$\beta$). Statistically significant differences between pairs of distributions are marked with # (R vs. G).