An Elementary Introduction to Information Geometry
- PMID: 33286868
- PMCID: PMC7650632
- DOI: 10.3390/e22101100
An Elementary Introduction to Information Geometry
Abstract
In this survey, we describe the fundamental differential-geometric structures of information manifolds, state the fundamental theorem of information geometry, and illustrate some use cases of these information manifolds in information sciences. The exposition is self-contained by concisely introducing the necessary concepts of differential geometry. Proofs are omitted for brevity.
Keywords: Bayesian hypothesis testing; Fisher–Rao distance; Hessian manifolds; affine connection; conjugate connections; curvature and flatness; differential geometry; dual metric-compatible parallel transport; dually flat manifolds; exponential family; gauge freedom; information manifold; metric compatibility; metric tensor; mixed parameterization; mixture clustering; mixture family; parameter divergence; separable divergence; statistical divergence; statistical invariance; statistical manifold; α-embeddings.
Conflict of interest statement
The author declare no conflict of interest.
Figures










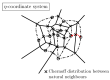

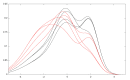
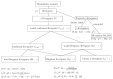
References
-
- Shannon C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27:623–656. doi: 10.1002/j.1538-7305.1948.tb00917.x. - DOI
-
- Amari S. Information Geometry and Its Applications. Springer; Tokyo, Japan: 2016. Applied Mathematical Sciences.
-
- Kakihara S., Ohara A., Tsuchiya T. Information Geometry and Interior-Point Algorithms in Semidefinite Programs and Symmetric Cone Programs. J. Optim. Theory Appl. 2013;157:749–780. doi: 10.1007/s10957-012-0180-9. - DOI
-
- Amari S., Nagaoka H. Methods of Information Geometry. American Mathematical Society; Providence, RL, USA: 2007.
-
- Peirce C.S. Chance, Love, and Logic: Philosophical Essays. U of Nebraska Press; Lincoln, NE, USA: 1998.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

