Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Oct 29;22(11):1231.
doi: 10.3390/e22111231.

Information Processing in the Brain as Optimal Entropy Transport: A Theoretical Approach

Carlos Islas  1 , Pablo Padilla  2 , Marco Antonio Prado  1   2
Affiliations

Information Processing in the Brain as Optimal Entropy Transport: A Theoretical Approach

Carlos Islas et al. Entropy (Basel). .

Abstract

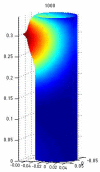
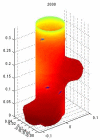
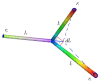
We consider brain activity from an information theoretic perspective. We analyze the information processing in the brain, considering the optimality of Shannon entropy transport using the Monge-Kantorovich framework. It is proposed that some of these processes satisfy an optimal transport of informational entropy condition. This optimality condition allows us to derive an equation of the Monge-Ampère type for the information flow that accounts for the branching structure of neurons via the linearization of this equation. Based on this fact, we discuss a version of Murray's law in this context.

Keywords: Monge–Ampère equation; Murray’s law; informational entropy; neuronal branching structures; neuroscience; optimal transport; variational calculus.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Numerical solution of the linearization of the Monge-Ampère equation including growth. Branching occurs when there is the concentration of the solution, the morphogen, above a certain threshold (the color code stands for standard heat maps: red, high; blue, low). This simulation was provided by Jorge Castillo-Medina and developed in COMSOL. For more details, the reader is referred to [21] and the references therein.
Figure 2
Figure 2
A similar simulation as in the previous figure with a different growth rate. Notice the different branching structure. Simulation performed by J. Castillo as well; see also [21].
Figure 3
Figure 3
The figure shows schematically the geometric configuration when branching occurs on a plane. Illustration after [33] by the authors.
See this image and copyright information in PMC

References

    1. Jensen G., Ward R.D., Balsam P.D. Information: Theory, brain, and behavior. J. Exp. Anal. Behav. 2013;100:408–431. doi: 10.1002/jeab.49. - DOI - PMC - PubMed
    1. Pregowska A., Szczepanski J., Wajnryb E. Temporal code versus rate code for binary Information Sources. Neurocomputing. 2016;216:756–762. doi: 10.1016/j.neucom.2016.08.034. - DOI
    1. Pregowska A., Szczepanski J., Wajnryb E. How Far can Neural Correlations Reduce Uncertainty? Comparison of Information Transmission Rates for Markov and Bernoulli Processes. Int. J. Neural Syst. 2019;29:1950003. doi: 10.1142/S0129065719500035. - DOI - PubMed
    1. Harris J.J., Jolivet R., Engl E., Attwell D. Energy-Efficient Information Transfer by Visual Pathway Synapses. Curr. Biol. 2015;25:3151–3160. doi: 10.1016/j.cub.2015.10.063. - DOI - PMC - PubMed
    1. Harris J.J., Engl E., Attwell D., Jolivet R.B. Energy-efficient information transfer at thalamocortical synapses. PLoS Comput. Biol. 2019;15:1–27. doi: 10.1371/journal.pcbi.1007226. - DOI - PMC - PubMed

LinkOut - more resources