Lag-invariant detection of interactions in spatially-extended systems using linear inverse modeling
- PMID: 33306719
- PMCID: PMC7732350
- DOI: 10.1371/journal.pone.0242715
Lag-invariant detection of interactions in spatially-extended systems using linear inverse modeling
Abstract
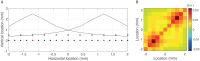
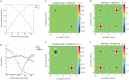
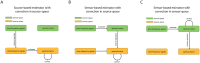
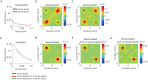
Measurements on physical systems result from the systems' activity being converted into sensor measurements by a forward model. In a number of cases, inversion of the forward model is extremely sensitive to perturbations such as sensor noise or numerical errors in the forward model. Regularization is then required, which introduces bias in the reconstruction of the systems' activity. One domain in which this is particularly problematic is the reconstruction of interactions in spatially-extended complex systems such as the human brain. Brain interactions can be reconstructed from non-invasive measurements such as electroencephalography (EEG) or magnetoencephalography (MEG), whose forward models are linear and instantaneous, but have large null-spaces and high condition numbers. This leads to incomplete unmixing of the forward models and hence to spurious interactions. This motivated the development of interaction measures that are exclusively sensitive to lagged, i.e. delayed interactions. The drawback of such measures is that they only detect interactions that have sufficiently large lags and this introduces bias in reconstructed brain networks. We introduce three estimators for linear interactions in spatially-extended systems that are uniformly sensitive to all lags. We derive some basic properties of and relationships between the estimators and evaluate their performance using numerical simulations from a simple benchmark model.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

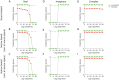
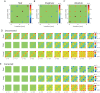
Similar articles
-
Reconstructing coherent networks from electroencephalography and magnetoencephalography with reduced contamination from volume conduction or magnetic field spread.PLoS One. 2013 Dec 2;8(12):e81553. doi: 10.1371/journal.pone.0081553. eCollection 2013. PLoS One. 2013. PMID: 24349088 Free PMC article.
-
Phase shift invariant imaging of coherent sources (PSIICOS) from MEG data.Neuroimage. 2018 Dec;183:950-971. doi: 10.1016/j.neuroimage.2018.08.031. Epub 2018 Aug 22. Neuroimage. 2018. PMID: 30142449
-
Localization of extended brain sources from EEG/MEG: the ExSo-MUSIC approach.Neuroimage. 2011 May 1;56(1):102-13. doi: 10.1016/j.neuroimage.2011.01.054. Epub 2011 Jan 27. Neuroimage. 2011. PMID: 21276860
-
Automated model selection in covariance estimation and spatial whitening of MEG and EEG signals.Neuroimage. 2015 Mar;108:328-42. doi: 10.1016/j.neuroimage.2014.12.040. Epub 2014 Dec 23. Neuroimage. 2015. PMID: 25541187
-
Effect of Field Spread on Resting-State Magneto Encephalography Functional Network Analysis: A Computational Modeling Study.Brain Connect. 2017 Nov;7(9):541-557. doi: 10.1089/brain.2017.0525. Epub 2017 Oct 27. Brain Connect. 2017. PMID: 28875718
Cited by
-
Towards a more robust non-invasive assessment of functional connectivity.Imaging Neurosci (Camb). 2024 Mar 28;2:imag-2-00119. doi: 10.1162/imag_a_00119. eCollection 2024. Imaging Neurosci (Camb). 2024. PMID: 40800450 Free PMC article.
-
Characterization of Second-Order Mixing Effects in Reconstructed Cross-Spectra of Random Neural Fields.Brain Topogr. 2024 Sep;37(5):647-658. doi: 10.1007/s10548-024-01040-8. Epub 2024 Mar 12. Brain Topogr. 2024. PMID: 38472533 Free PMC article.
-
Relation between the phase-lag index and lagged coherence for assessing interactions in EEG and MEG data.Neuroimage Rep. 2021 Apr 21;1(1):100007. doi: 10.1016/j.ynirp.2021.100007. eCollection 2021 Mar. Neuroimage Rep. 2021. PMID: 40568236 Free PMC article.
References
-
- Rizkallah J, Amoud H, Fraschini M, Wendling F, Hassan M. Removing zero-lag functional connections can alter EEG-source space networks at rest. bioRxiv. 2019; 10.1101/617118. - DOI
-
- Hindriks R, Micheli C, Mantini D, Deco G. Human resting-state electrophysiological networks in the alpha frequency band: Evidence from magnetoencephalographic source imaging. bioRxiv. 2017;.
-
- Hämäläinen M, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography, instrumentation, and applications to noninvasive studies of the working human brain. Reviews of Modern Physics. 1993;65(2):413–497. 10.1103/RevModPhys.65.413 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

