Explaining the effects of distractor statistics in visual search
- PMID: 33331851
- PMCID: PMC7746958
- DOI: 10.1167/jov.20.13.11
Explaining the effects of distractor statistics in visual search
Abstract
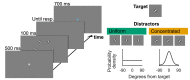
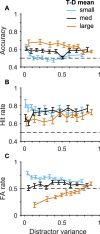
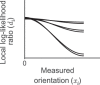
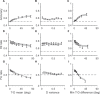
Visual search, the task of detecting or locating target items among distractor items in a visual scene, is an important function for animals and humans. Different theoretical accounts make differing predictions for the effects of distractor statistics. Here we use a task in which we parametrically vary distractor items, allowing for a simultaneously fine-grained and comprehensive study of distractor statistics. We found effects of target-distractor similarity, distractor variability, and an interaction between the two, although the effect of the interaction on performance differed from the one expected. To explain these findings, we constructed computational process models that make trial-by-trial predictions for behavior based on the stimulus presented. These models, including a Bayesian observer model, provided excellent accounts of both the qualitative and quantitative effects of distractor statistics, as well as of the effect of changing the statistics of the environment (in the form of distractors being drawn from a different distribution). We conclude with a broader discussion of the role of computational process models in the understanding of visual search.
Figures







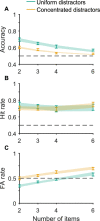

Similar articles
-
Dwelling on distractors varying in target-distractor similarity.Acta Psychol (Amst). 2019 Jul;198:102859. doi: 10.1016/j.actpsy.2019.05.011. Epub 2019 Jun 15. Acta Psychol (Amst). 2019. PMID: 31212105
-
A salient and task-irrelevant collinear structure hurts visual search.PLoS One. 2015 Apr 24;10(4):e0124190. doi: 10.1371/journal.pone.0124190. eCollection 2015. PLoS One. 2015. PMID: 25909986 Free PMC article.
-
Effect of task set-modulating attentional capture depends on the distractor cost in visual search: evidence from N2pc.Neuroreport. 2014 Jul 9;25(10):737-42. doi: 10.1097/WNR.0000000000000163. Neuroreport. 2014. PMID: 24840929
-
Priming of probabilistic attentional templates.Psychon Bull Rev. 2023 Feb;30(1):22-39. doi: 10.3758/s13423-022-02125-w. Epub 2022 Jul 13. Psychon Bull Rev. 2023. PMID: 35831678 Review.
-
Foraging behavior in visual search: A review of theoretical and mathematical models in humans and animals.Psychol Res. 2022 Mar;86(2):331-349. doi: 10.1007/s00426-021-01499-1. Epub 2021 Mar 21. Psychol Res. 2022. PMID: 33745028 Review.
Cited by
-
Neural Processing of Noise-Vocoded Speech Under Divided Attention: An fMRI-Machine Learning Study.Hum Brain Mapp. 2025 Aug 1;46(11):e70312. doi: 10.1002/hbm.70312. Hum Brain Mapp. 2025. PMID: 40772490 Free PMC article.
-
Perceptual Learning of Noise-Vocoded Speech Under Divided Attention.Trends Hear. 2023 Jan-Dec;27:23312165231192297. doi: 10.1177/23312165231192297. Trends Hear. 2023. PMID: 37547940 Free PMC article.
-
Perceptual adaptation to dysarthric speech is modulated by concurrent phonological processing: A dual task study.J Acoust Soc Am. 2025 Mar 1;157(3):1598-1611. doi: 10.1121/10.0035883. J Acoust Soc Am. 2025. PMID: 40063084 Free PMC article.
-
Classic Visual Search Effects in an Additional Singleton Task: An Open Dataset.J Cogn. 2021 Jul 28;4(1):34. doi: 10.5334/joc.182. eCollection 2021. J Cogn. 2021. PMID: 34396037 Free PMC article.
-
How do (perceptual) distracters distract?PLoS Comput Biol. 2022 Oct 13;18(10):e1010609. doi: 10.1371/journal.pcbi.1010609. eCollection 2022 Oct. PLoS Comput Biol. 2022. PMID: 36228038 Free PMC article.
References
-
- Acerbi L. & Ma W. J. (2017). Practical Bayesian optimization for model fitting with Bayesian adaptive direct search. In Advances in Neural Information Processing Systems 30 (pp. 1836–1846). Retrieved from http://papers.nips.cc/paper/6780-practical-bayesian-optimization-for-mod....
-
- Afshartous D. & Preston R. A. (2011). Key results of interaction models with centering. Journal of Statistics Education, 19(3), doi:10.1080/10691898.2011.11889620. - DOI
-
- Berens P. (2009). CircStat: A MATLAB toolbox for circular statistics. Journal of Statistical Software, 31(10), 1–21, doi:10.18637/jss.v031.i10. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

