Generalized Solutions of Parrondo's Games

Abstract

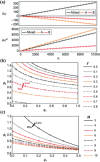
In game theory, Parrondo's paradox describes the possibility of achieving winning outcomes by alternating between losing strategies. The framework had been conceptualized from a physical phenomenon termed flashing Brownian ratchets, but has since been useful in understanding a broad range of phenomena in the physical and life sciences, including the behavior of ecological systems and evolutionary trends. A minimal representation of the paradox is that of a pair of games played in random order; unfortunately, closed-form solutions general in all parameters remain elusive. Here, we present explicit solutions for capital statistics and outcome conditions for a generalized game pair. The methodology is general and can be applied to the development of analytical methods across ratchet-type models, and of Parrondo's paradox in general, which have wide-ranging applications across physical and biological systems.

Keywords: Brownian ratchets; Parrondo's paradox; analytical methods; game theory; generalized solutions; noise; non‐linear dynamics.

Figure 1

Comparison of $\mathrm{\Delta }\mu$ and $\mathrm{\Delta }{\sigma }^2$ from theory and simulations across $p_1-p_2$ parameter space, for differing $M$. Relative error between theory and simulation is $<0.1$% throughout. Phase diagrams are also shown; background colors represent theory and dots represent simulation. Dotted lines denote theoretical boundaries, for $\mathrm{\Delta }{\mu }_R=\mathrm{\Delta }{\mu }_B$ (black), $\mathrm{\Delta }{\mu }_R=\mathrm{\Delta }{\mu }_A$ (gray), $\mathrm{\Delta }{\mu }_R=0$ (red), and $\mathrm{\Delta }{\mu }_B=0$ (blue). Parameters are $p=0.39$, $r=r_1=r_2=0.2$, $\gamma =0.5$.

Figure 2

a) Plot of $\mu (n)$ and ${\sigma }^2(n)$ comparing theory (lines) and simulation (circles), realizing the strong Parrondo effect. Parameters are $p=0.39$, $p_1=0.02$, $p_2=0.6$, $r=r_1=r_2=0.2$, and $\gamma =0.5$. b,c) $\mathrm{\Delta }\mu =0$ fair isoclines in ${\varphi }_1$‐${\varphi }_2$ parameter space for differing $M$ and $\gamma$, comparing theory (lines) and simulation (circles). Parameters are $p_1=0.35$ and $r=r_1=r_2=0.1$, with $M=4$ for (b) and $\gamma =0.5$ for (c).

Figure 3

a) Theoretical results on $\mathrm{\Delta }\mu$ and $\mathrm{\Delta }{\sigma }^2$ across $p_i$ parameter space for $M=4$. The full parameter space is 4D and cannot be directly illustrated; slices across $p_i-p_2-p_3$ space are shown, for two values of $p_4$. To preserve visual clarity, simulation results are not plotted, but relative error is $<0.1$% throughout. Parameters are $p=0.39$, $r=r_i=0.2$ for $i\in [1,4]$, and $\gamma =0.5$. b) $\mathrm{\Delta }\mu$ and $\mathrm{\Delta }{\sigma }^2$ from theory and simulations across $p$–$\gamma$ parameter space, and phase plot, where background colors represent theory and dots represent simulation. Dotted lines denote theoretical boundaries, for $\mathrm{\Delta }{\mu }_{\mathcal{R}}=\mathrm{\Delta }{\mu }_{\mathcal{B}}$ (black), $\mathrm{\Delta }{\mu }_{\mathcal{R}}=\mathrm{\Delta }{\mu }_{\mathcal{A}}$ (gray), $\mathrm{\Delta }{\mu }_{\mathcal{R}}=0$ (red), and $\mathrm{\Delta }{\mu }_{\mathcal{A}}=0$ (blue). Parameters are $r=r_i=0.2$, $p_1=0.02$, and $p_i=0.5$ for $i\in [2,6]$.