Forward-looking serial intervals correctly link epidemic growth to reproduction numbers

Abstract

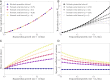
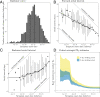
The reproduction number R and the growth rate r are critical epidemiological quantities. They are linked by generation intervals, the time between infection and onward transmission. Because generation intervals are difficult to observe, epidemiologists often substitute serial intervals, the time between symptom onset in successive links in a transmission chain. Recent studies suggest that such substitution biases estimates of R based on r. Here we explore how these intervals vary over the course of an epidemic, and the implications for R estimation. Forward-looking serial intervals, measuring time forward from symptom onset of an infector, correctly describe the renewal process of symptomatic cases and therefore reliably link R with r. In contrast, backward-looking intervals, which measure time backward, and intrinsic intervals, which neglect population-level dynamics, give incorrect R estimates. Forward-looking intervals are affected both by epidemic dynamics and by censoring, changing in complex ways over the course of an epidemic. We present a heuristic method for addressing biases that arise from neglecting changes in serial intervals. We apply the method to early (21 January to February 8, 2020) serial interval-based estimates of R for the COVID-19 outbreak in China outside Hubei province; using improperly defined serial intervals in this context biases estimates of initial R by up to a factor of 2.6. This study demonstrates the importance of early contact tracing efforts and provides a framework for reassessing generation intervals, serial intervals, and R estimates for COVID-19.

Keywords: generation interval; infectious disease modeling; reproduction number; serial interval.

Fig. 1.

Illustration of intrinsic, forward, and backward serial intervals. (A) The intrinsic serial interval for a cohort of individuals infected at time $p$. In this case, ${\tau }_{\mathrm{\text{i1}}}$ is drawn from the intrinsic incubation period distribution, ${\tau }_g$ is drawn from the intrinsic generation interval distribution, and ${\tau }_{\mathrm{\text{i2}}}$ is drawn from the intrinsic incubation period distribution. (B) The forward serial interval for a cohort of infectors who became symptomatic at time $p$. In this case, ${\tau }_{\mathrm{\text{i1}}}$ is drawn from the backward incubation period distribution, ${\tau }_g$ is drawn from the forward generation interval distribution, and ${\tau }_{\mathrm{\text{i2}}}$ is drawn from the forward incubation period distribution. (C) The backward serial interval for a cohort of infectees who became symptomatic at time s. In this case, ${\tau }_{\mathrm{\text{i1}}}$ is drawn from the forward incubation period distribution, ${\tau }_g$ is drawn from the backward generation interval distribution, and ${\tau }_{\mathrm{\text{i2}}}$ is drawn from the backward incubation period distribution. Intrinsic intervals (black) reflect average of individual characteristics and are not dependent on population-level dynamics. Forward intervals (green) can change due to epidemiological dynamics (e.g., contraction of generation intervals through susceptible depletion). Backward intervals (blue) can change due to changes in cohort sizes even when forward intervals remain time invariant.

Fig. 2.

Estimates of the reproduction number from the exponential growth rate based on serial and generation interval distributions. (A) The initial forward serial interval distributions give the correct link between the exponential growth rate $r$ and the reproduction number ${\mathcal{R}}_0$, for any correlation $\rho$ between intrinsic incubation period and intrinsic generation interval of the underlying bivariate log-normal distribution. (B) The intrinsic serial interval distributions give an incorrect link between $r$ and ${\mathcal{R}}_0$. (C) The mean initial forward serial interval during the exponential growth phase increases with $r$. (D) The squared coefficient of variation of the initial forward serial intervals during the exponential growth phase decreases with $r$.

Fig. 3.

Epidemiological dynamics and changes in mean forward and backward delay distributions. (A) Daily incidence over time. (B–D) Changes in the mean forward incubation period, generation interval, and serial interval. (E–G) Changes in the mean backward incubation period, generation interval, and serial interval. Black (A) and colored (B–G) lines represent the results of a deterministic simulation. Gray lines (A) represent the results of 10 stochastic simulations. Colored points (B–G) represent the average of 10 stochastic simulations. Dashed lines represent the mean initial forward delay. Forward and backward delays are colored according to Fig. 1. In order to remove possible transient dynamics (e.g., left censoring of time delays and initial stochasticity due to low number of infections), we set $t=0$ to the first time point when daily incidence is greater than 100. Intrinsic incubation periods and intrinsic generation intervals are assumed to be independent of each other, for simplicity. See SI Appendix, Fig. S1 for simulations with correlated incubation periods and generation intervals. See Table 1 for parameter values.

Fig. 4.

Estimating the reproduction number from the observed serial intervals. (A) Schematic representation of line list data collected during an epidemic. (B) Estimates of ${\mathcal{R}}_0$ based on all observed serial intervals completed by a given time. (C) Schematic representation of line list data rearranged by symptom onset date of infectors. (D) Estimates of ${\mathcal{R}}_0$ based on all observed serial intervals started by a given time. Black dashed lines represent the mean initial forward serial interval and ${\mathcal{R}}_0$. Black solid lines represent the mean intrinsic serial interval and ${\mathcal{R}}_{\mathrm{\text{intrinsic}}}$. Colored solid lines represent the mean estimates of ${\mathcal{R}}_0$ across 10 stochastic simulations. Colored ribbons represent the range of estimates of ${\mathcal{R}}_0$ across 10 stochastic simulations.

Fig. 5.

Observed serial intervals of COVID-19 and cohort-averaged estimates of $\mathcal{R}$. (A) Symptom onset dates of all individuals within 468 transmission pairs included in the contact tracing data. (B and C) Forward and backward serial intervals over time. Serial interval data have been grouped based on the symptom onset dates of primary (B) and secondary (C) cases. Points represent the means. Vertical error bars represent the 95% equitailed quantiles. Solid lines represent the estimated locally estimated scatterplot smoothing fits. The dashed lines represent the maximum and minimum observable delays across the range of reported symptom onset dates. (D) Cohort-averaged estimates of ${\mathcal{R}}_0$ assuming doubling period of 6 and 8 d (14, 39). Ribbons represent the associated 95% bootstrap CIs. The data were taken from supplementary materials of ref. .