2D Zernike polynomial expansion: Finding the protein-protein binding regions

Abstract

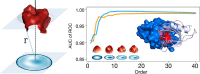
We present a method for efficiently and effectively assessing whether and where two proteins can interact with each other to form a complex. This is still largely an open problem, even for those relatively few cases where the 3D structure of both proteins is known. In fact, even if much of the information about the interaction is encoded in the chemical and geometric features of the structures, the set of possible contact patches and of their relative orientations are too large to be computationally affordable in a reasonable time, thus preventing the compilation of reliable interactome. Our method is able to rapidly and quantitatively measure the geometrical shape complementarity between interacting proteins, comparing their molecular iso-electron density surfaces expanding the surface patches in term of 2D Zernike polynomials. We first test the method against the real binding region of a large dataset of known protein complexes, reaching a success rate of 0.72. We then apply the method for the blind recognition of binding sites, identifying the real region of interaction in about $60\%$ of the analyzed cases. Finally, we investigate how the efficiency in finding the right binding region depends on the surface roughness as a function of the expansion order.

Keywords: Molecular surface; Protein-protein interactions; Shape complementarity.

Graphical abstract

Fig. 1

Surface patch decomposition in the 2D Zernike basis. a) Molecular representation of a protein surface. The red region highlights a possible patch. b) Each patch is first oriented along the z-axis, then a cone is build such that all surface points are contained inside the cone. c) 2D projection of the patch. The origin of such cone is used to assign the color in the plane, as the distance between the origin and each point of the surface. d) Zernike invariant associated to the selected patch. Each invariant is defined as the modulus of the coefficients obtained projecting the patch against the Zernike basis. e) Surface reconstruction at different orders.

Fig. 2

Parameter variation. a) Performance, measured by the AUC of the ROC curve, in discriminating the real binding region against a set of random patches from the Protein Dataset (see Methods), upon varying the patch radius, $R_s$ and the expansion order, n of the Zernike basis. b) AUC of the ROC as a function of the expansion order for four fixed values of $R_s$. c) AUC of the ROC as a function of the patch radius, $R_s$ for four fixed values of n.

Fig. 3

Blind identification of the binding regions. a) Overlap, AUC of the ROC and AUC of the PR for the first ten percentiles of the Protein dataset when order by size of the complexes. For all three descriptors, red (respectively blue) bars correspond to proteins for which the binding region is (resp. is not) correctly identified by the complemetarity-driven blind search as described in text. b) Sketch of the three possible representation of the binding region (left) obtained by the Zernike expansion: depending on the expansion order, n. c) Surface and cartoon representation of three example complexes, colored according to the binding propensity. From top to bottom the roughness (see Eq. 7) of the real binding region decreases. d) AUC of the ROC vs Roughness for the first ten percentiles of the Protein Dataset ordered by size. Points are colored according to the size of the corresponding protein. e) AUC of the ROC as a function of the expansion order for the three examples of panel c).

Fig. 4

Analysis of the three descriptors. a) Comparison between the $O_d$ of the two proteins forming the complexes of the first ten percentiles of the Protein Dataset ordered by size (left). The same for AUC of the ROC curve (center) and AUC of the PR curve (right) b) $O_d$ of the smaller 50 proteins of the Protein Dataset for different rounds of smoothing.