Population Pharmacodynamic Modeling Using the Sigmoid Emax Model: Influence of Inter-individual Variability on the Steepness of the Concentration-Effect Relationship. a Simulation Study

Abstract

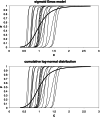
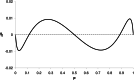
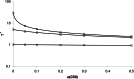
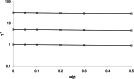
The relationship between the concentration of a drug and its pharmacological effect is often described by empirical mathematical models. We investigated the relationship between the steepness of the concentration-effect relationship and inter-individual variability (IIV) of the parameters of the sigmoid E_max model, using the similarity between the sigmoid E_max model and the cumulative log-normal distribution. In addition, it is investigated whether IIV in the model parameters can be estimated accurately by population modeling. Multiple data sets, consisting of 40 individuals with 4 binary observations in each individual, were simulated with varying values for the model parameters and their IIV. The data sets were analyzed using Excel Solver and NONMEM. An empirical equation (Eq. (11)) was derived describing the steepness of the population-predicted concentration-effect profile (γ*) as a function of γ and IIV in C50 and γ, and was validated for both binary and continuous data. The tested study design is not suited to estimate the IIV in C50 and γ with reasonable precision. Using a naive pooling procedure, the population estimates γ* are significantly lower than the value of γ used for simulation. The steepness of the population-predicted concentration-effect relationship (γ*) is less than that of the individuals (γ). Using γ*, the population-predicted drug effect represents the drug effect, for binary data the probability of drug effect, at a given concentration for an arbitrary individual.

Keywords: inter-individual variability; pharmacokinetic-pharmacodynamic modeling; sigmoid Emax model; simulation.

Fig. 1

Concentration–P relationship of 20 simulated individuals (thin lines) using the sigmoid E_max model (upper panel) and cumulative log-normal distribution (lower panel. Typical individual (dashed line) and population prediction (solid line). C50 = 1 (arbitrary unit); γ = 30 (sigmoid E_max model); σ = 0.0567 (cumulative log-normal distribution); ω_C50 = 0.1; ω_γ = 0.1

Fig. 2

Difference (ΔP) between the profiles of P obtained with sigmoid E_max model and P obtained with cumulative log-normal distribution, using γ* = 5.27 calculated using Eq. (11) and σ* = 0.323 using Eq. (10), respectively. Parameter values as in Fig. 1: C50 = 1 (arbitrary unit); γ = 30 (sigmoid E_max model); σ = 0.0567 (cumulative log-normal distribution); ω_C50 = 0.1; ω_γ = 0.1

Fig. 3

Relationship between γ* and ω_C50 obtained by Monte Carlo simulation (open symbols), and the model prediction using Eq. (11) (solid lines), for γ = 1 (lower line and symbols), 5 and 30 (upper line and symbols) and ω_γ = 0

Fig. 4

Relationship between γ* and ω_γ obtained by Monte Carlo simulation (open symbols), and the model prediction using Eq. (11) (solid lines), for γ = 1 (lower line and symbols), 5 and 30 (upper line and symbols) and ω_C50 = 0