Estimation of non-constant variance in isothermal titration calorimetry using an ITC measurement model
- PMID: 33378411
- PMCID: PMC7773272
- DOI: 10.1371/journal.pone.0244739
Estimation of non-constant variance in isothermal titration calorimetry using an ITC measurement model
Abstract
Isothermal titration calorimetry (ITC) is the gold standard for accurate measurement of thermodynamic parameters in solution reactions. In the data processing of ITC, the non-constant variance of the heat requires special consideration. The variance function approach has been successfully applied in previous studies, but is found to fail under certain conditions in this work. Here, an explicit ITC measurement model consisting of main thermal effects and error components has been proposed to quantitatively evaluate and predict the non-constant variance of the heat data under various conditions. Monte Carlo simulation shows that the ITC measurement model provides higher accuracy and flexibility than variance function in high c-value reactions or with additional error components, for example, originated from the fluctuation of the concentrations or other properties of the solutions. The experimental design of basic error evaluation is optimized accordingly and verified by both Monte Carlo simulation and experiments. An easy-to-run Python source code is provided to illustrate the establishment of the ITC measurement model and the estimation of heat variances. The accurate and reliable non-constant variance of heat is helpful to the application of weighted least squares regression, the proper evaluation or selection of the reaction model.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

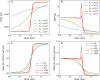

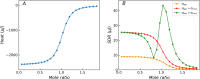

Similar articles
-
Evaluation and Minimization of Uncertainty in ITC Binding Measurements: Heat Error, Concentration Error, Saturation, and Stoichiometry.Biochim Biophys Acta Gen Subj. 2017 Feb;1861(2):485-498. doi: 10.1016/j.bbagen.2016.09.002. Epub 2016 Sep 15. Biochim Biophys Acta Gen Subj. 2017. PMID: 27599357 Free PMC article.
-
Statistical error in isothermal titration calorimetry: variance function estimation from generalized least squares.Anal Biochem. 2005 Aug 1;343(1):106-15. doi: 10.1016/j.ab.2005.04.026. Anal Biochem. 2005. PMID: 15936713
-
A study of statistical error in isothermal titration calorimetry.Anal Biochem. 2003 Oct 1;321(1):79-88. doi: 10.1016/s0003-2697(03)00406-8. Anal Biochem. 2003. PMID: 12963058
-
Isothermal titration calorimetry: experimental design, data analysis, and probing macromolecule/ligand binding and kinetic interactions.Methods Cell Biol. 2008;84:79-113. doi: 10.1016/S0091-679X(07)84004-0. Methods Cell Biol. 2008. PMID: 17964929 Review.
-
Thermodynamics of protein-ligand interactions: history, presence, and future aspects.J Recept Signal Transduct Res. 2004 Feb;24(1-2):1-52. doi: 10.1081/rrs-120037896. J Recept Signal Transduct Res. 2004. PMID: 15344878 Review.
Cited by
-
Protocols for protein-DNA binding analysis of a zinc finger transcription factor bound to its cognate promoter.STAR Protoc. 2022 Jul 31;3(3):101598. doi: 10.1016/j.xpro.2022.101598. eCollection 2022 Sep 16. STAR Protoc. 2022. PMID: 35928006 Free PMC article.
-
An Orthogonal Workflow of Electrochemical, Computational, and Thermodynamic Methods Reveals Limitations of Using a Literature-Reported Insulin Binding Peptide in Biosensors.ACS Omega. 2024 Sep 5;9(37):39219-39231. doi: 10.1021/acsomega.4c06481. eCollection 2024 Sep 17. ACS Omega. 2024. PMID: 39310205 Free PMC article.
-
Predicting the Key Properties of a Modified Product to Pre-Select a Pluronic F127 Modification Scheme for Preparing High-Quality Nano-Micelles.Polymers (Basel). 2025 Jan 27;17(3):349. doi: 10.3390/polym17030349. Polymers (Basel). 2025. PMID: 39940552 Free PMC article.
References
-
- Hansen LD, Transtrum MK, Quinn CF. Titration Calorimetry: Springer; 2018.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

