Boltzmann Machines as Generalized Hopfield Networks: A Review of Recent Results and Outlooks

Abstract

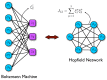
The Hopfield model and the Boltzmann machine are among the most popular examples of neural networks. The latter, widely used for classification and feature detection, is able to efficiently learn a generative model from observed data and constitutes the benchmark for statistical learning. The former, designed to mimic the retrieval phase of an artificial associative memory lays in between two paradigmatic statistical mechanics models, namely the Curie-Weiss and the Sherrington-Kirkpatrick, which are recovered as the limiting cases of, respectively, one and many stored memories. Interestingly, the Boltzmann machine and the Hopfield network, if considered to be two cognitive processes (learning and information retrieval), are nothing more than two sides of the same coin. In fact, it is possible to exactly map the one into the other. We will inspect such an equivalence retracing the most representative steps of the research in this field.

Keywords: boltzmann machine; hopfield model; statistical mechanics of disordered systems.

Figure 1

Schematic representation of the equivalence between a two-layer HRBM (left) and an Hopfield network (right). Please note that the size of the visible layer (here $N=6$) and of the hidden layer (here $P=3$) in the former correspond, respectively, to the size and to the number of stored patterns in the latter.

Figure 2

Phase diagram of a generalized RBM for varying pattern, hidden and visible unit priors as found in [12]. In all plots, the yellow region represents the ergodic phase, the red region represents the spin-glass phase, and the blue region represents the retrieval phase. First line: the visible units are Boolean and ${\Omega }_z=1$. In this case the retrieval region approaches the line $\alpha =0$ and $T\in [0,{\Omega }_z]$ as $\delta \to 0$. Second line: the visible variables are Boolean and $\delta =1$. The retrieval region approaches the line $T=0$ and $\alpha \in [0,{\alpha }_c\left(\delta \right)]$ as ${\Omega }_z\to 0$. Third line: $\delta =1$, ${\Omega }_z=1$ and the soft visible units are regularized with a spherical constraint. As ${\Omega }_{\sigma }\to 0$ the retrieval region approaches low load values.

Figure 3

Examples of typical graphs obtained for different values of c and $\alpha$; in any case the size is $N=4000$. Left: a picture corresponding to the under-percolated regime ($\alpha =0.4,c=1$). Middle: a picture corresponding to the percolation threshold ($\alpha =c=1$). Right: a picture corresponding to the over-percolated regime ($\alpha =0.1,c=5$). Notice that isolated nodes are not depicted.

Figure 4

The phase diagram is depicted for different choices of t, namely, from left to right, $t=0,1,1000$. Notice that, as t grows, the retrieval region (blue) and the ergodic region (yellow) become larger and larger while the spin-glass region (red) shrinks up to collapse as $t\to \infty$. A change in the concavity of the critical line separating the ergodic region and the spin-glass region is also observed.