Computing the Rearrangement Distance of Natural Genomes
- PMID: 33393848
- PMCID: PMC8082732
- DOI: 10.1089/cmb.2020.0434
Computing the Rearrangement Distance of Natural Genomes
Abstract
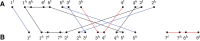
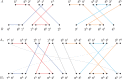
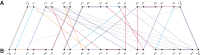
The computation of genomic distances has been a very active field of computational comparative genomics over the past 25 years. Substantial results include the polynomial-time computability of the inversion distance by Hannenhalli and Pevzner in 1995 and the introduction of the double cut and join distance by Yancopoulos et al. in 2005. Both results, however, rely on the assumption that the genomes under comparison contain the same set of unique markers (syntenic genomic regions, sometimes also referred to as genes). In 2015, Shao et al. relax this condition by allowing for duplicate markers in the analysis. This generalized version of the genomic distance problem is NP-hard, and they give an integer linear programming (ILP) solution that is efficient enough to be applied to real-world datasets. A restriction of their approach is that it can be applied only to balanced genomes that have equal numbers of duplicates of any marker. Therefore, it still needs a delicate preprocessing of the input data in which excessive copies of unbalanced markers have to be removed. In this article, we present an algorithm solving the genomic distance problem for natural genomes, in which any marker may occur an arbitrary number of times. Our method is based on a new graph data structure, the multi-relational diagram, that allows an elegant extension of the ILP by Shao et al. to count runs of markers that are under- or over-represented in one genome with respect to the other and need to be inserted or deleted, respectively. With this extension, previous restrictions on the genome configurations are lifted, for the first time enabling an uncompromising rearrangement analysis. Any marker sequence can directly be used for the distance calculation. The evaluation of our approach shows that it can be used to analyze genomes with up to a few 10,000 markers, which we demonstrate on simulated and real data.
Keywords: DCJ-indel distance; comparative genomics; genome rearrangements.
Conflict of interest statement
The authors declare they have no conflicting financial interests.
Figures




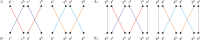



References
-
- Angibaud, S., Fertin, G., Rusu, I., et al. . 2009. On the approximability of comparing genomes with duplicates. (A preliminary version appeared in Proc. of WALCOM 2008.) J. Graph Alg. Appl. 13, 19–53
-
- Bergeron, A., Mixtacki, J., and Stoye, J.. 2006. A unifying view of genome rearrangements. In Proceedings of the 6th International Conference on Algorithms in Bioinformatics (WABI 2006). Volume 4175 of LNBI, Springer Verlag, Berlin-Heidelberg, pp. 163–173
-
- Bohnenkämper, L., Braga, M.D.V., Doerr, D., et al. . 2020. Computing the rearrangement distance of natural genomes. In Schwartz, R., ed., Proceedings of the 24th International Conference on Research in Computational Molecular Biology, RECOMB 2020. Volume 12074 of LNCS, Springer Verlag, Cham, pp. 3–18
-
- Braga, M.D.V., and Stoye, J.. 2010. The solution space of sorting by DCJ. (A preliminary version appeared in Proc. of RECOMB-CG 2009.) J. Comput. Biol. 17, 1145–1165 - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
