Toward an Information Theory of Quantitative Genetics

Abstract

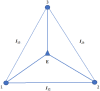
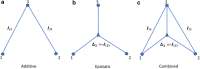
Quantitative genetics has evolved dramatically in the past century, and the proliferation of genetic data, in quantity as well as type, enables the characterization of complex interactions and mechanisms beyond the scope of its theoretical foundations. In this article, we argue that revisiting the framework for analysis is important and we begin to lay the foundations of an alternative formulation of quantitative genetics based on information theory. Information theory can provide sensitive and unbiased measures of statistical dependencies among variables, and it provides a natural mathematical language for an alternative view of quantitative genetics. In the previous work, we examined the information content of discrete functions and applied this approach and methods to the analysis of genetic data. In this article, we present a framework built around a set of relationships that both unifies the information measures for the discrete functions and uses them to express key quantitative genetic relationships. Information theory measures of variable interdependency are used to identify significant interactions, and a general approach is described for inferring functional relationships in genotype and phenotype data. We present information-based measures of the genetic quantities: penetrance, heritability, and degrees of statistical epistasis. Our scope here includes the consideration of both two- and three-variable dependencies and independently segregating variants, which captures additive effects, genetic interactions, and two-phenotype pleiotropy. This formalism and the theoretical approach naturally apply to higher multivariable interactions and complex dependencies, and can be adapted to account for population structure, linkage, and nonrandomly segregating markers. This article thus focuses on presenting the initial groundwork for a full formulation of quantitative genetics based on information theory.

Keywords: entropy; epistasis; genetics; information theory.

FIG. 1.

Three-variable dependencies that make up the multi-information or total correlation (we adopt the convention here that X is 1, Y is 2, and Z is 3). The lines represent the components of dependence among the variables (small circles) as in the above equation, where the epistatic component is represented by the lines emanating from the triangle. The epistatic component is E = −I₁₂₃+S.

FIG. 2.

Independent segregation interaction relationships. The genetic contributions of 1 and 2 to the phenotype, 3, illustrating the distinction between the additive (a) and epistatic (b) effects within a relationship with a combined effect (c).

FIG. 3.

Function classes (3 × 3) on the landscape. Each spot in both panels represents a function class, or family. (a) The information landscape shows the orientation of the plane with respect to the 3D landscape. (b) A set of 12 panels, one each for the complete set of possible values of the multi-information, Ω, for the 3 × 3 functions. The plane is the projected diagonal plane of the 3D landscape, the gray spots are the same for each panel and show the positions of all of the families of functions. The red spots are the families specific for each specific value of Ω. The upper left panel has no function as the information content of the uniform functions is zero, and all Δ's are zero. 3D, three-dimensional.

FIG. 4.

The information plane for haploid genetics, binary genetic variables. The color-coded points show the locations of the function families corresponding to the alphabet size of the phenotype, as indicated in the legend panel at the top right. Families 1–4 correspond to a binary phenotype alphabet. Families 5–7 are added for a three-letter alphabet, and family 8 is added for a four-letter alphabet. The blue dot in the legend is not seen since it does not correspond to any specific family. The five-letter alphabet functions all fall into the previous eight families. While the limit is eight families, as the alphabet size increases the number of functions in every family grows. The families 1, 2, 5, 6, and 8 are functions with only pairwise interactions (δ_Z = 0).

FIG. 5.

Analysis of simulated data. (a) These are values of the penetrance calculated for 50 simulated data sets each for 9 values of penetrance, p. For all of these values, except the two right-most (p = 0.2 and p = 0.1), the greedy algorithm returned the exact function. (b) For these two there were a few errors in the function (top panel is correct function), as shown in these examples for two cases of p = 0.1 simulations (the errors are highlighted).

FIG. 6.

Four of the 16 2 × 2 genetic models show protective effects. The functions are shown in linear form and color coded according to the families as marked on the information plane.

FIG. 7.

The pairwise peaks for the genetic determinants of two phenotypes. The locations indicated are the chromosomal coordinates of the highest scoring marker in the peak.

FIG. 10.

Phenotype distributions by genotype. We examined the tuple with the highest value of 0 for the neomycin phenotype: loci chrXIII_319136 and chrXIV_371336. The panels show the phenotype distribution for each genotype (e.g., plot 01 shows samples with chrXIII_319136 = 0 and chrXIV_371336 = 1).

FIG. 8.

Genetic effects for two growth phenotypes. The full genome is shown with the single- and two-locus effects. The pairwise peaks for these phenotypes, as shown in Figure 7, are indicated as the red curves in the black band (using all 28,820 markers.) The variant pair interaction effects for these phenotypes are indicated by the internal red lines (all interacting pairs are shown in the Appendix Tables D1 and D2) indicating the significant three-way dependencies between the two markers at the ends of the line and the phenotype, indicating genetic loci interacting. (a) Genetics of growth on neomycin and (b) growth on copper sulfate.

FIG. 9.

Epistatic fractions compared. The bars represent the fractional epistatic effect for the interactions in the order listed in Appendix Tables D1 and D2. For brevity, the marker indicated below each bar is the one listed in the left-hand column of the tables, and represents the pair.

FIG. 11.

Evaluating statistical significance of the epistatic effect for pair of loci chrXIII_319136 and chrXIV_371336. The distribution of 10,000 epistatic fractions calculated on permuted trials. The actual epistatic fraction is indicated by the dotted line.