Coherence resonance in influencer networks

Abstract

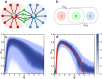
Complex networks are abundant in nature and many share an important structural property: they contain a few nodes that are abnormally highly connected (hubs). Some of these hubs are called influencers because they couple strongly to the network and play fundamental dynamical and structural roles. Strikingly, despite the abundance of networks with influencers, little is known about their response to stochastic forcing. Here, for oscillatory dynamics on influencer networks, we show that subjecting influencers to an optimal intensity of noise can result in enhanced network synchronization. This new network dynamical effect, which we call coherence resonance in influencer networks, emerges from a synergy between network structure and stochasticity and is highly nonlinear, vanishing when the noise is too weak or too strong. Our results reveal that the influencer backbone can sharply increase the dynamical response in complex systems of coupled oscillators.

Fig. 1. Coherence resonance in an influencer network.

Distribution of the order parameter R versus the effective diffusion q in the influencers. a Influencers a and b are hubs that couple strongly to the network, and all other nodes are regarded as followers. Three distinct partitions of followers are shown in red, blue, and green, which connect to influencer a, b, and both a and b, respectively. In our simulation, each partition has 300 followers. b Mean-field theory predicts that the interactions of the partition mean-fields take place in a hyper-graph mediated by the coupling functions G_a and G_b see Methods. c, d For each value of effective noise strength q in the influencers, we plot the density of the global order parameter R on a color scale from 0 (white) to the maximum value (dark blue). At an optimal noise strength, the mean value of the global order parameter reaches a maximum, revealing the coherence resonance effect. In c the dynamical frequency gap between influencers and followers ΔΩ/λ₀ = 18 is moderate, whereas in d ΔΩ/λ₀ = 198 is large. The solid red line in c is our analytical prediction.

Fig. 2. Coherence resonance of the order parameter in different complex networks.

a–c, e–g The time series of the order parameter R for three values of noise strength in the influencers for weak q = 0.1 (a, e), optimal q = 1 (b, f), and strong q = 10 (c, g). d, h show the corresponding networks with d a scale-free network with exponent 2 and h C. elegans directed neural network. See Methods for further details. Additional examples can be found in Supplementary Note 5.