Optimal surveillance mitigation of COVID'19 disease outbreak: Fractional order optimal control of compartment model

Abstract

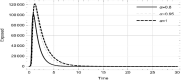
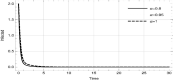
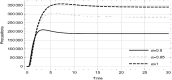
In present time, the whole world is in the phase of war against the deadly pandemic COVID'19 and working on different interventions in this regard. Variety of strategies are taken into account from ground level to the state to reduce the transmission rate. For this purpose, the epidemiologists are also augmenting their contribution in structuring such models that could depict a scheme to diminish the basic reproduction number. These tactics also include the awareness campaigns initiated by the stakeholders through digital, print media and etc. Analyzing the cost and profit effectiveness of these tactics, we design an optimal control dynamical model to study the proficiency of each strategy in reducing the virulence of COVID'19. The aim is to illustrate the memory effect on the dynamics of COVID'19 with and without prevention measures through fractional calculus. Therefore, the structure of the model is in line with generalized proportional fractional derivative to assess the effects at each chronological change. Awareness about using medical mask, social distancing, frequent use of sanitizer or cleaning hand and supportive care during treatment are the strategies followed worldwide in this fight. Taking these into consideration, the optimal objective function proposed for the surveillance mitigation of COVID'19, is contemplated as the cost function. The effect analysis is supported through graphs and tabulated values. In addition, sensitivity inspection of basic reproduction number is also carried out with respect to different values of fractional index and cost function. Ultimately, social distancing and supportive care of infected are found to be significant in decreasing the basic reproduction number more rapidly.

Keywords: COVID'19; Fractional derivative; Hamiltonian; Optimal control; Stability.

Fig. 1

Pictorial illustration of SEQIMRP model.

Fig. 2

Sensitivity inspection of $R_0$ with respect to $\mathit{mm}$ and $\mathit{sd}$ for $\mathit{ch}=0.1,sc=0.1$, at $\alpha =0.95$.

Fig. 3

Sensitivity inspection of $R_0$ with respect to $\mathit{ch}$ and $\mathit{sd}$ for $\mathit{mm}=0.1,sc=0.1$, at $\alpha =0.95$.

Fig. 4

Sensitivity inspection of $R_0$ with respect to $\mathit{ch}$ and $\mathit{sc}$ for $\mathit{mm}=0.1,sd=0.1$, at $\alpha =0.95$.

Fig. 5

Sensitivity inspection of $R_0$ with respect to $\mathit{ch}$ and $\mathit{mm}$ for $\mathit{sd}=0.1,sc=0.1$, at $\alpha =0.95$.

Fig. 6

Sensitivity inspection of $R_0$ with respect to $\mathit{sd}$ and $\mathit{sc}$ for $\mathit{mm}=0.1,ch=0.1$, at $\alpha =0.95$.

Fig. 7

Sensitivity inspection of $R_0$ with respect to $\mathit{mm}$ and $\mathit{sc}$ for $\mathit{sd}=0.1,ch=0.1$, at $\alpha =0.95$.

Fig. 8

Dynamics of $S\left(t\right)\in {\mathrm{\Pi }}_2$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0,sd=0,ch=0$ and $\mathit{sc}=0$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 9

Dynamics of $E\left(t\right)\in {\mathrm{\Pi }}_2$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0,sd=0,ch=0$ and $\mathit{sc}=0$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 10

Dynamics of $Q\left(t\right)\in {\mathrm{\Pi }}_2$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0,sd=0,ch=0$ and $\mathit{sc}=0$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 11

Dynamics of $I\left(t\right)\in {\mathrm{\Pi }}_2$ of SEQIMRP, for parameters described in Table 1 for $\mathit{mm}=0,sd=0,ch=0$ and $\mathit{sc}=0$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 12

Dynamics of $M\left(t\right)\in {\mathrm{\Pi }}_2$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0,sd=0,ch=0$ and $\mathit{sc}=0$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 13

Dynamics of $R\left(t\right)\in {\mathrm{\Pi }}_2$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0,sd=0,ch=0$ and $\mathit{sc}=0$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 14

Dynamics of $P\left(t\right)\in {\mathrm{\Pi }}_2$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0,sd=0,ch=0$ and $\mathit{sc}=0$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 15

Dynamics of $S\left(t\right)\in {\mathrm{\Pi }}_1$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0.2,sd=0.3,ch=0.35$ and $\mathit{sc}=0.65$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 16

Dynamics of $E\left(t\right)\in {\mathrm{\Pi }}_1$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0.2,sd=0.3,ch=0.35$ and $\mathit{sc}=0.65$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 17

Dynamics of $Q\left(t\right)\in {\mathrm{\Pi }}_1$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0.2,sd=0.3,ch=0.35$ and $\mathit{sc}=0.65$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 18

Dynamics of $I\left(t\right)\in {\mathrm{\Pi }}_1$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0.2,sd=0.3,ch=0.35$ and $\mathit{sc}=0.65$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 19

Dynamics of $M\left(t\right)\in {\mathrm{\Pi }}_1$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0.2,sd=0.3,ch=0.35$ and $\mathit{sc}=0.65$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 20

Dynamics of $R\left(t\right)\in {\mathrm{\Pi }}_1$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0.2,sd=0.3,ch=0.35$ and $\mathit{sc}=0.65$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.

Fig. 21

Dynamics of $P\left(t\right)\in {\mathrm{\Pi }}_1$ of SEQIMRP, for parameters described in Table 1 and $\mathit{mm}=0.2,sd=0.3,ch=0.35$ and $\mathit{sc}=0.65$, at $\alpha =0.8,0.95,1$and $t\in \left[0,30\right]$.