Reconstructing Genotypes in Private Genomic Databases from Genetic Risk Scores
- PMID: 33400590
- PMCID: PMC8165474
- DOI: 10.1089/cmb.2020.0445
Reconstructing Genotypes in Private Genomic Databases from Genetic Risk Scores
Abstract
Some organizations such as 23andMe and the UK Biobank have large genomic databases that they re-use for multiple different genome-wide association studies. Even research studies that compile smaller genomic databases often utilize these databases to investigate many related traits. It is common for the study to report a genetic risk score (GRS) model for each trait within the publication. Here, we show that under some circumstances, these GRS models can be used to recover the genetic variants of individuals in these genomic databases-a reconstruction attack. In particular, if two GRS models are trained by using a largely overlapping set of participants, it is often possible to determine the genotype for each of the individuals who were used to train one GRS model, but not the other. We demonstrate this theoretically and experimentally by analyzing the Cornell Dog Genome database. The accuracy of our reconstruction attack depends on how accurately we can estimate the rate of co-occurrence of pairs of single nucleotide polymorphisms within the private database, so if this aggregate information is ever released, it would drastically reduce the security of a private genomic database. Caution should be applied when using the same database for multiple analysis, especially when a small number of individuals are included or excluded from one part of the study.
Keywords: GWAS; genetic risk scores; genomic privacy; long-term privacy; reconstruction attack.
Conflict of interest statement
The authors declare they have no competing financial interests.
Figures



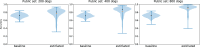
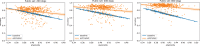

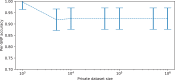
References
-
- Celeux, G., and Diebolt, J.. 1985. The SEM algorithm: A probabilistic teacher algorithm derived from the EM algorithm for the mixture problem. Comput. Stat. Q. 2, 73–82
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
