Response theory and phase transitions for the thermodynamic limit of interacting identical systems
- PMID: 33402877
- PMCID: PMC7776973
- DOI: 10.1098/rspa.2020.0688
Response theory and phase transitions for the thermodynamic limit of interacting identical systems
Abstract
We study the response to perturbations in the thermodynamic limit of a network of coupled identical agents undergoing a stochastic evolution which, in general, describes non-equilibrium conditions. All systems are nudged towards the common centre of mass. We derive Kramers-Kronig relations and sum rules for the linear susceptibilities obtained through mean field Fokker-Planck equations and then propose corrections relevant for the macroscopic case, which incorporates in a self-consistent way the effect of the mutual interaction between the systems. Such an interaction creates a memory effect. We are able to derive conditions determining the occurrence of phase transitions specifically due to system-to-system interactions. Such phase transitions exist in the thermodynamic limit and are associated with the divergence of the linear response but are not accompanied by the divergence in the integrated autocorrelation time for a suitably defined observable. We clarify that such endogenous phase transitions are fundamentally different from other pathologies in the linear response that can be framed in the context of critical transitions. Finally, we show how our results can elucidate the properties of the Desai-Zwanzig model and of the Bonilla-Casado-Morillo model, which feature paradigmatic equilibrium and non-equilibrium phase transitions, respectively.
Keywords: Bonilla–Casado–Morilla model; Desai–Zwanzig model; Kramers–Kronig relations; order–disorder transitions; sum rules; thermodynamic limit.
© 2020 The Authors.
Conflict of interest statement
We declare we have no competing interests.
Figures
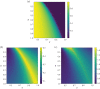
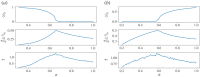
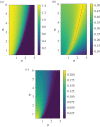
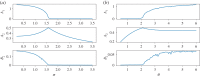
Similar articles
-
Spectroscopy of phase transitions for multiagent systems.Chaos. 2021 Jun;31(6):061103. doi: 10.1063/5.0053558. Chaos. 2021. PMID: 34241317
-
Dynamics of the Desai-Zwanzig model in multiwell and random energy landscapes.Phys Rev E. 2019 Mar;99(3-1):032109. doi: 10.1103/PhysRevE.99.032109. Phys Rev E. 2019. PMID: 30999473
-
Kramers-Kronig relations and sum rules in nonlinear optical spectroscopy.Appl Spectrosc. 2004 May;58(5):499-509. doi: 10.1366/000370204774103309. Appl Spectrosc. 2004. PMID: 15165324
-
Recent developments in the kinetic theory of nucleation.Adv Colloid Interface Sci. 2005 Dec 30;118(1-3):51-72. doi: 10.1016/j.cis.2005.06.001. Epub 2005 Aug 30. Adv Colloid Interface Sci. 2005. PMID: 16137628 Review.
-
Landauer Bound and Continuous Phase Transitions.Entropy (Basel). 2023 Jun 28;25(7):984. doi: 10.3390/e25070984. Entropy (Basel). 2023. PMID: 37509932 Free PMC article. Review.
References
-
- Dawson DA. 1983. Critical dynamics and fluctuations for a mean-field model of cooperative behavior. J. Stat. Phys. 31, 29–85. (10.1007/BF01010922) - DOI
-
- Acebrón JA, Bonilla LL, Pérez Vicente CJ, Ritort F, Spigler R. 2005. The kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185. (10.1103/RevModPhys.77.137) - DOI
-
- Garnier J, Papanicolaou G, Yang T. 2013. Large deviations for a mean field model of systemic risk. SIAM J. Financ. Math. 4, 151–184. (10.1137/12087387X) - DOI
-
- Wang C, Li Q, B. Chazelle WE. 2017. Noisy Hegselmann-Krause systems: phase transition and the 2r-conjecture. J. Stat. Phys. 166, 1209–1225. (10.1007/s10955-017-1718-x) - DOI
-
- Garnier J, Papanicolaou G, Yang T. 2017. Consensus convergence with stochastic effects. Vietnam J. Math. 45, 51–75. (10.1007/s10013-016-0190-2) - DOI
LinkOut - more resources
Full Text Sources

