Improving probabilistic infectious disease forecasting through coherence
- PMID: 33406068
- PMCID: PMC7837472
- DOI: 10.1371/journal.pcbi.1007623
Improving probabilistic infectious disease forecasting through coherence
Abstract
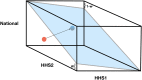
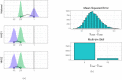
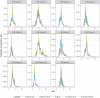
With an estimated $10.4 billion in medical costs and 31.4 million outpatient visits each year, influenza poses a serious burden of disease in the United States. To provide insights and advance warning into the spread of influenza, the U.S. Centers for Disease Control and Prevention (CDC) runs a challenge for forecasting weighted influenza-like illness (wILI) at the national and regional level. Many models produce independent forecasts for each geographical unit, ignoring the constraint that the national wILI is a weighted sum of regional wILI, where the weights correspond to the population size of the region. We propose a novel algorithm that transforms a set of independent forecast distributions to obey this constraint, which we refer to as probabilistically coherent. Enforcing probabilistic coherence led to an increase in forecast skill for 79% of the models we tested over multiple flu seasons, highlighting the importance of respecting the forecasting system's geographical hierarchy.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

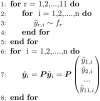



References
-
- Thompson M, Shay D, Zhou H, Bridges C, Cheng P, Burns E, et al. Estimates of deaths associated with seasonal influenza-United States, 1976-2007. Morbidity and Mortality Weekly Report. 2010;59(33):1057–1062. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

