NETWORK CLASSIFICATION WITH APPLICATIONS TO BRAIN CONNECTOMICS
- PMID: 33408802
- PMCID: PMC7785130
- DOI: 10.1214/19-AOAS1252
NETWORK CLASSIFICATION WITH APPLICATIONS TO BRAIN CONNECTOMICS
Abstract
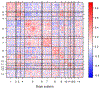
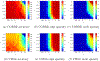
While statistical analysis of a single network has received a lot of attention in recent years, with a focus on social networks, analysis of a sample of networks presents its own challenges which require a different set of analytic tools. Here we study the problem of classification of networks with labeled nodes, motivated by applications in neuroimaging. Brain networks are constructed from imaging data to represent functional connectivity between regions of the brain, and previous work has shown the potential of such networks to distinguish between various brain disorders, giving rise to a network classification problem. Existing approaches tend to either treat all edge weights as a long vector, ignoring the network structure, or focus on graph topology as represented by summary measures while ignoring the edge weights. Our goal is to design a classification method that uses both the individual edge information and the network structure of the data in a computationally efficient way, and that can produce a parsimonious and interpretable representation of differences in brain connectivity patterns between classes. We propose a graph classification method that uses edge weights as predictors but incorporates the network nature of the data via penalties that promote sparsity in the number of nodes, in addition to the usual sparsity penalties that encourage selection of edges. We implement the method via efficient convex optimization and provide a detailed analysis of data from two fMRI studies of schizophrenia.
Keywords: fMRI data; graph classification; high-dimensional data; variable selection.
Figures

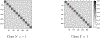

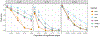


References
-
- Aine CJ, Bockholt HJ, Bustillo JR, Cañive JM, Caprihan A, Gasparovic C, Hanlon FM, Houck JM, Jung RE, Lauriello J, Liu J, Mayer AR, Perrone-Bizzozero NI, Posse S, Stephen JM, Turner JA, Clark VP, and Calhoun VD (2017). Multimodal neuroimaging in schizophrenia: Description and dissemination. Neuroinformatics, 15(4):343–364. - PMC - PubMed
-
- American Psychiatric Association (1994). Diagnostic and statistical manual of mental disorders (DSM). Washington, DC: American Psychiatric Association.
-
- Bach F, Jenatton R, Mairal J, and Obozinski G (2012). Structured sparsity through convex optimization. Statistical Science, 27(4):450–468.
-
- Bach FR (2008). Consistency of the group lasso and multiple kernel learning. Journal of Machine Learning Research, 9(Jun):1179–1225.
-
- Beck A and Teboulle M (2009). A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2(1):183–202.
Grants and funding
LinkOut - more resources
Full Text Sources
