Extracting the dynamics of behavior in sensory decision-making experiments
- PMID: 33412101
- PMCID: PMC7897255
- DOI: 10.1016/j.neuron.2020.12.004
Extracting the dynamics of behavior in sensory decision-making experiments
Abstract
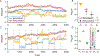
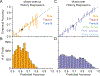
Decision-making strategies evolve during training and can continue to vary even in well-trained animals. However, studies of sensory decision-making tend to characterize behavior in terms of a fixed psychometric function that is fit only after training is complete. Here, we present PsyTrack, a flexible method for inferring the trajectory of sensory decision-making strategies from choice data. We apply PsyTrack to training data from mice, rats, and human subjects learning to perform auditory and visual decision-making tasks. We show that it successfully captures trial-to-trial fluctuations in the weighting of sensory stimuli, bias, and task-irrelevant covariates such as choice and stimulus history. This analysis reveals dramatic differences in learning across mice and rapid adaptation to changes in task statistics. PsyTrack scales easily to large datasets and offers a powerful tool for quantifying time-varying behavior in a wide variety of animals and tasks.
Keywords: behavioral dynamics; learning; psychophysics; sensory decision making.
Copyright © 2020 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures




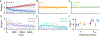

Comment in
-
Neuroscience needs behavior: inferring psychophysical strategy trial by trial.Neuron. 2021 Feb 17;109(4):561-563. doi: 10.1016/j.neuron.2021.01.025. Neuron. 2021. PMID: 33600750
References
-
- Akrami A, Kopec CD, Diamond ME, Brody CD, 2018. Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 554, 368. - PubMed
-
- Bak JH, Choi JY, Akrami A, Witten I, Pillow JW, 2016. Adaptive optimal training of animal behavior, in: Advances in Neural Information Processing Systems, pp. 1947–1955.
-
- Bak JH, Pillow JW, 2018. Adaptive stimulus selection for multi-alternative psychometric functions with lapses. Journal of Vision 18, 4 URL: +␣10.1167/18.12.4, doi:10.1167/18.12.4, arXiv:/data/journals/jov/937613/i1534-7362-18-12-4.pdf. - DOI - DOI - PMC - PubMed
-
- Bishop CM, 2006. Pattern recognition and machine learning. Springer.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

