From Transcript to Tissue: Multiscale Modeling from Cell Signaling to Matrix Remodeling
- PMID: 33415527
- PMCID: PMC8260704
- DOI: 10.1007/s10439-020-02713-8
From Transcript to Tissue: Multiscale Modeling from Cell Signaling to Matrix Remodeling
Abstract
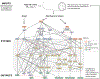
Tissue-level biomechanical properties and function derive from underlying cell signaling, which regulates mass deposition, organization, and removal. Here, we couple two existing modeling frameworks to capture associated multiscale interactions-one for vessel-level growth and remodeling and one for cell-level signaling-and illustrate utility by simulating aortic remodeling. At the vessel level, we employ a constrained mixture model describing turnover of individual wall constituents (elastin, intramural cells, and collagen), which has proven useful in predicting diverse adaptations as well as disease progression using phenomenological constitutive relations. Nevertheless, we now seek an improved mechanistic understanding of these processes; we replace phenomenological relations in the mixture model with a logic-based signaling model, which yields a system of ordinary differential equations predicting changes in collagen synthesis, matrix metalloproteinases, and cell proliferation in response to altered intramural stress, wall shear stress, and exogenous angiotensin II. This coupled approach promises improved understanding of the role of cell signaling in achieving tissue homeostasis and allows us to model feedback between vessel mechanics and cell signaling. We verify our model predictions against data from the hypertensive murine infrarenal abdominal aorta as well as results from validated phenomenological models, and consider effects of noisy signaling and heterogeneous cell populations.
Keywords: Constrained mixtures; Growth and remodeling; Homeostasis; Logic-based modeling; Mechanobiology.
© 2021. Biomedical Engineering Society.
Figures


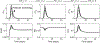
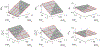



References
-
- Apaŕıcio P, Thompson MS, and Watton PN. A novel chemo-mechanobiological model of arterial tissue growth and remodelling. Journal of Biomechanics, 49(12):2321–2330, 2016. - PubMed
MeSH terms
Grants and funding
- R01 HL146723/NH/NIH HHS/United States
- U01 HL142518/NH/NIH HHS/United States
- U01 HL142518/HL/NHLBI NIH HHS/United States
- R01 HL139796/NH/NIH HHS/United States
- R01 HL105297/HL/NHLBI NIH HHS/United States
- R01 HL139796/HL/NHLBI NIH HHS/United States
- P01 HL134605/NH/NIH HHS/United States
- R01 HL146723/HL/NHLBI NIH HHS/United States
- P01 HL134605/HL/NHLBI NIH HHS/United States
- R01 HL105297/NH/NIH HHS/United States
- R01 HL105297/NH/NIH HHS/United States
- P01 HL134605/NH/NIH HHS/United States
- R01 HL139796/NH/NIH HHS/United States
- U01 HL142518/NH/NIH HHS/United States
- R01 HL146723/NH/NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources

