All or nothing belief updating in patients with schizophrenia reduces precision and flexibility of beliefs

Abstract

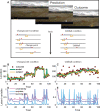
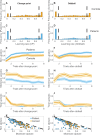
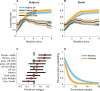
Schizophrenia is characterized by abnormal perceptions and beliefs, but the computational mechanisms through which these abnormalities emerge remain unclear. One prominent hypothesis asserts that such abnormalities result from overly precise representations of prior knowledge, which in turn lead beliefs to become insensitive to feedback. In contrast, another prominent hypothesis asserts that such abnormalities result from a tendency to interpret prediction errors as indicating meaningful change, leading to the assignment of aberrant salience to noisy or misleading information. Here we examine behaviour of patients and control subjects in a behavioural paradigm capable of adjudicating between these competing hypotheses and characterizing belief updates directly on individual trials. We show that patients are more prone to completely ignoring new information and perseverating on previous responses, but when they do update, tend to do so completely. This updating strategy limits the integration of information over time, reducing both the flexibility and precision of beliefs and provides a potential explanation for how patients could simultaneously show over-sensitivity and under-sensitivity to feedback in different paradigms.

Keywords: belief updating; computational psychiatry; learning; schizophrenia.

Figure 1

A modified predictive inference task to measure behavioural adjustment in response to surprising outcomes. (A) In each trial, participants moved a bucket to the location at which they expected a helicopter (obscured by clouds) to drop a bag of potentially rewarding contents (top left). After the participant indicated satisfaction with the bucket placement, a bag fell from the top of the screen, which provided new information about the true location of the helicopter (in the bag location; top middle) and about the reward attained on that trial (in the amount of the bag contents that landed in the bucket; top right). All participants completed the task under two different generative conditions that were explicitly instructed. In the change-point condition (bottom left) the helicopter position occasionally underwent change-points, leading to a persistent change in the location of bags (red circles) across trials (vertical axis). In the oddball condition (bottom right) the bag location was occasionally unrelated to the actual helicopter location, giving rise to oddball events that were unrelated to bag positions preceding or following them. (B and C) Bucket placements made by an example subject (yellow) and the normative model (green) for each trial (abscissa) of a task block in which bag locations (red points) were generated using either a change-point (B) or oddball (C) structure. Note that model and example subject behaviour includes rapid behavioural adjustment in response to large errors in predicted bag location for the change-point condition (B), but not in the oddball condition (C). (D and E) Behaviour of the normative model is described by an error-driven learning rule in which the learning rate (purple) is adjusted in each trial according to uncertainty about the current helicopter position (pink) and surprise (blue), as indexed by the posterior probability with which a particular outcome was generated as a consequence of an unlikely generative event such as a change-point (D) or oddball (E). The model is fully aware of the generative environments and thus increases learning from surprising information when in the change-point context (D) but decreases learning from surprising information in the oddball context (E).

Figure 2

Schizophrenia patients do not display heightened sensitivity to unlikely events. (A) Synthetic updating behaviour generated by a normative model (yellow) and the same model equipped with a heightened sensitivity to detect unlikely events, implemented in the normative framework as an abnormally high prior on such events (hazard rate; blue) was regressed onto prediction errors in sliding windows of absolute prediction error magnitude (x-axis). The resulting slope, termed the learning rate (y-axis), increases with prediction error magnitude in the change-point condition (lighter colours) but decreases with prediction error magnitude in the oddball condition (darker colours). Higher hazard rate (blue) leads to a leftward shift in both curves, reflecting a higher sensitivity to small changes in prediction error, particularly for moderate prediction error magnitudes. (B) Patient (blue) and control (yellow) participant learning (y-axis), assessed in the same manner, displays a qualitatively similar bifurcation of learning in the two conditions (dark = oddball, light = change-point) with increased prediction error magnitude (x-axis); however, patient curves are not shifted leftward with respect to control curves, as would be predicted by an increased hazard rate. There is not a leftward shift of the blue curves relative to the yellow (as would be expected under the high hazard rate hypothesis) nor is there a consistent offset in the learning rate of patients relative to controls (compare blue and yellow on ordinate). However, across conditions there was a modest reduction of learning rates in patients relative to controls [mean/SEM learning rate for patients: 0.34/0.02 and controls: 0.41/0.03, t(124) = −2.0, P = 0.04]. CP = change-point.

Figure 3

Schizophrenia patients make moderate updates less frequently than matched controls. (A–D) Learning rate frequency histograms depicting the relative frequency with which controls (A and B) and patients (C and D) used specific single trial learning rates (x-axis) in the change-point (CP) (A and C) and oddball (B and D) conditions. Dotted lines indicate thresholds used to group single trial learning rates into non-updating (left), moderate updating (middle), and total updating (right) categories. (E and F) Mean/SEM (lines/shading) frequency of non-updating in patients (blue) and controls (yellow) is plotted as a function of the number of trials after a change-point (E) or oddball (F). (G and H) Mean/SEM (lines/shading) frequency of moderate updating in patients (blue) and controls (yellow) is plotted as a function of the number of trials after a change-point (G) or oddball (H). Patients used moderate updates less frequently, and non-updates more frequently than controls [mean/SEM moderate updates for patients: 0.33/0.02 and controls: 0.45/0.02, t(124) = −4.1, P = 7 × 10⁻⁵; mean/SEM non updates for patients: 0.49/0.02 and controls: 0.37/0.03, t(124) = 3.3, P = 0.001]. (I and J) Mean/SEM (lines/shading) frequency of total updating in patients (blue) and controls (yellow) is plotted as a function of the number of trials after a change-point (I) or oddball (J). There was no statistical difference in total updates between the groups [mean/SEM total updates for patients: 0.15/0.02 and controls: 0.16/0.02, t(124) = −0.4, P = 0.66]. (K and L) Mean non-update frequency (y-axis) is plotted against moderate update frequency (x-axis) for individual patients (blue points) and controls (yellow points) in change-point (K) and oddball (L) conditions.

Figure 4

Patients rely more on total updates, particularly when uncertain. (A) For participants who used higher learning rates on average (x-axis), a greater proportion of learning was attributable to discrete total updates (single trial learning rates >0.9; y-axis). For any given average learning rate, patients (blue) tended to be more reliant on total updates than were controls (orange). Points reflect individual subject and lines reflect least squares fits to separate groups. (B) Coefficients (y-axis) reflecting the contribution of patient status to predictions about the frequency of discrete bins of single trial learning rate (x-axis). Positive/negative values indicate more/less frequent use of a particular category of learning rate by patients after controlling for average rate of learning. Line/shading reflects mean/95% confidence intervals and asterisks reflect significant differences from zero after false discovery rate correction (P < 0.005). (C) Control participants used more moderate updates (blue, y-axis), but not more total updates (red) on trials in which the normative model indicated a high level of uncertainty (x-axis). (D) Patients increased both moderate (blue) and total (red) updates as a function of uncertainty.

Figure 5

Learning rate sequences used by schizophrenia patients yield beliefs that are both less flexible and less precise than those of control subjects. (A) Schematic depicting the effects of a non-update (left), moderate update (middle), and total update (right) on the precision of an underlying belief distribution. In all cases bucket placement is initialized to a prior outcome (x; t − 2) and is updated in accordance with the most recent one (blue dot; t − 1). The degree of updating used by the agent affects the weight of previous outcomes on the updated bucket position, with the non-update leading to complete reliance on the t-2 bag position, the total update relying completely on the t − 1 bag position, and the moderate update equally weighting these two sources of information (second row). Computing precision of the resulting belief distribution yields a value twice as large for the moderate update than the other two updating strategies, which we quantify as containing two effective samples, as opposed to only a single effective sample in the case of a non-update or total update. (B) Single trial learning rates (LR) can be used to calculate the relative weight (y-axis) attributed to previous outcomes at any lag (x-axis). Applying this method to synthetic learning behaviour yields a geometric distribution for fixed learning rate models (blue, yellow) that is unaffected by change-points in the generative structure of the task (depicted by the dotted line at lag −5). In contrast, normative learning models (green) approximate a uniform weight distribution across all lags occurring after the previous change-point but do not assign weight to trials occurring prior to the most recent change-point (dotted line). Flexible belief updating requires that beliefs are based on only relevant information, that is, that all weight is given to trials occurring since the last change-point. (C) The precision of a belief on a given trial can be computed according to weight attribution profile that gave rise to it. The precision, which can be measured in units of effective samples, increases to an asymptotic value for fixed learning rate models (yellow and blue) but changes dynamically in the normative model (green)—growing almost linearly during periods of stability but rapidly collapsing to one after a recognized change-point. (D) Flexibility, as assessed by the proportion of belief weights attributed to outcomes in the relevant context (y-axis), increased as a function of trials after a change-point (x-axis) for controls (yellow) and patients (blue)—but was consistently higher for controls. (E) Precision, as assessed by the effective number of samples contributing to the reported belief (y-axis), also increased as a function of trials after a change-point (x-axis), and did so more rapidly for controls (yellow) than for patients (blue). (F) Differences in flexibility (proportion relevant weight) and precision (effective samples) were prominent in a large number of individual patients.

Figure 6

Direct model fitting suggests that patients use more non-updates than control participants. (A) Patients (blue) and controls (yellow) both tended to increase learning rate (y-axis) in response to surprising information (higher relative errors; x-axis) in the change-point (CP) condition (light colours), but decrease learning rate in response to surprising information in the oddball condition (dark colours). (B) Synthetic data from an extension of the normative model that was fit to patients (blue) and controls (yellow) mimic the reduced learning rate from small errors and the less extreme bifurcation observed in the empirical patient data. (C) Regression coefficients and 95% confidence intervals (points and lines; sorted by value) stipulating the contribution of each parameter estimated by the normative model to a logistic regression classifier of patient status. The two parameters governing the magnitude and shape of the perseverative response profile (Persev. Width, Persev. Max) made significant positive contributions to the classifier. (D) Perseveration probability as a function of the model-prescribed update is plotted separately for patients (blue) and controls (yellow). Note that perseveration did not differ uniformly across task conditions, but most prominently when the model prescribed making a relatively small update.