Inferring high-resolution human mixing patterns for disease modeling

Abstract

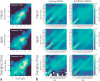
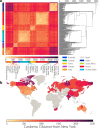
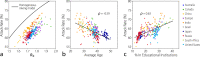
Mathematical and computational modeling approaches are increasingly used as quantitative tools in the analysis and forecasting of infectious disease epidemics. The growing need for realism in addressing complex public health questions is, however, calling for accurate models of the human contact patterns that govern the disease transmission processes. Here we present a data-driven approach to generate effective population-level contact matrices by using highly detailed macro (census) and micro (survey) data on key socio-demographic features. We produce age-stratified contact matrices for 35 countries, including 277 sub-national administratvie regions of 8 of those countries, covering approximately 3.5 billion people and reflecting the high degree of cultural and societal diversity of the focus countries. We use the derived contact matrices to model the spread of airborne infectious diseases and show that sub-national heterogeneities in human mixing patterns have a marked impact on epidemic indicators such as the reproduction number and overall attack rate of epidemics of the same etiology. The contact patterns derived here are made publicly available as a modeling tool to study the impact of socio-economic differences and demographic heterogeneities across populations on the epidemiology of infectious diseases.

Fig. 1. Modeling framework.

Schematic representation of the workflow for modeling human-mixing patterns and infection transmission dynamics.

Fig. 2. Age-mixing patterns by setting.

Each heatmap represents the average frequency of contact between an individual of a given age (x axis) and all of their possible contacts (y axis). a Matrices of household contacts by age at the national level for China, the United States, and India. The six smaller panels in the center and on the left show household contact matrices at the subnational level in two provinces of China (Beijing, Guizhou), two locations of the United States (the state of New York and the District of Columbia), and two states of India (Maharashtra, Meghalaya). b Matrices of school contacts by age at the national level (from top to bottom: China, the United States, India). c Matrices of work contacts by age at the national level (from top to bottom: China, the United States, India).

Fig. 3. Comparison to out-of-sample survey matrices.

a Density plots showing the correlation of survey-based contact matrices for three out-of-sample locations (France, Japan, and the Shanghai Province of China) and their respective synthetic contact matrices (all normalized to sum to one). The points represent the actual values of the survey and synthetic contact matrices. The linear correlation between the elements of each survey matrix and the corresponding elements of the synthetic matrix is reported in terms of the Pearson correlation coefficient, whose values are reported in each plot. b Heatmaps representing the normalized survey matrices and the normalized overall synthetic matrices for France, Japan, and the Shanghai Province of China.

Fig. 4. Overall contact matrices.

Each heatmap represents the overall average number of contacts relevant for airborne infectious disease transmission by age at the national level for China, the United States, and India.

Fig. 5. Clustering of contact matrices.

a Clustered matrix of the Canberra distance between subnational contact matrices and associated dendrogram using hierarchical clustering to organize subnational locations. Lighter colors indicate locations more similar to each other (distance closer to 0). b World map of the subnational level where colors represent the Canberra distance between each subnational location and the US state of New York (used as a reference point). The gray color means that no data is available. Note that the country of Israel is treated at the national level, rather than the subnational level, due to both its relatively small population and area, and the resolution of data available for reconstruction.

Fig. 6. Epidemic impact.

a Scatter plot of the attack rate and the reproduction number R₀ from an age-structured SIR model using the contact matrix for each subnational location. European countries are included. The black line shows the results of the classic homogeneous mixing SIR model (no age groups). b Scatter plot of attack rates and the average age in each location. The black line represents the best-fitting linear model demonstrating a negative linear correlation between attack rates and the average age of the population. c Scatter plot of attack rates and percentage of the population attending educational institutions in each location. The black line represents the best-fitting linear model.

Fig. 7. Subnational heterogeneity.

a The black dots represent the estimated attack rates in each province of China by using the country-level contact matrix and the location-specific age structure of the population. Colored dots represent the estimated attack rates in each location by using both the location-specific contact matrix and the age structure of the population. The colored lines connect the two estimated values of attack rate for each location. The transmission rate is set such that R₀ = 1.5 when using the country-level matrix. Each map shows the percentage variation of the attack rate using the location-specific contact matrix with respect to using the national contact matrix as a proxy for the subnational contact patterns (i.e., (AR_c − AR_l)/AR_c, where AR_c is the attack rate estimated by using the country-level contact matrix, and AR_l is that estimated by using the location-specific matrix). Colors toward Astra in the color scale indicate an overestimation of the attack rate in the location when using the country-level contact matrix as a proxy for the subnational contact patterns. Conversely, colors towards grape in the color scale indicate an underestimation of the attack rate in the location when using the country-level matrix as a proxy for the subnational contact patterns. b Same as a, but for the USA. c Same as a, but for India.