Computational modeling of human papillomavirus with impulsive vaccination
- PMID: 33437129
- PMCID: PMC7791917
- DOI: 10.1007/s11071-020-06123-2
Computational modeling of human papillomavirus with impulsive vaccination
Abstract
In this study, a new SIVS epidemic model for human papillomavirus (HPV) is proposed. The global dynamics of the proposed model are analyzed under pulse vaccination for the susceptible unvaccinated females and males. The threshold value for the disease-free periodic solution is obtained using the comparison theory for ordinary differential equations. It is demonstrated that the disease-free periodic solution is globally stable if the reproduction number is less than unity under some defined parameters. Moreover, we found the critical value of the pulse vaccination for susceptible females needed to control the HPV. The uniform persistence of the disease for some parameter values is also analyzed. The numerical simulations conducted agreed with the theoretical findings. It is found out using numerical simulation that the pulse vaccination has a good impact on reducing the disease.
Keywords: Global attractivity; Human papillomavirus; Impulsive vaccination; Uniform persistence.
© The Author(s), under exclusive licence to Springer Nature B.V. part of Springer Nature 2021.
Conflict of interest statement
Conflict of interestThe authors declare that they have no conflict of interests.
Figures
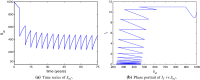
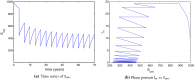

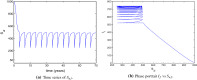
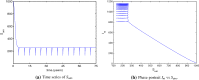
Similar articles
-
Threshold dynamics of a time-delayed SEIRS model with pulse vaccination.Math Biosci. 2015 Nov;269:178-85. doi: 10.1016/j.mbs.2015.09.005. Epub 2015 Sep 25. Math Biosci. 2015. PMID: 26408988
-
Analysis of risk-structured vaccination model for the dynamics of oncogenic and warts-causing HPV types.Bull Math Biol. 2014 Jul;76(7):1670-726. doi: 10.1007/s11538-014-9972-4. Epub 2014 Jul 18. Bull Math Biol. 2014. PMID: 25033777
-
Mathematical model for managing vector-borne pathogen outbreaks in chickens using impulsive vaccination and drug treatment.Sci Rep. 2024 Dec 30;14(1):31973. doi: 10.1038/s41598-024-83510-4. Sci Rep. 2024. PMID: 39738360 Free PMC article.
-
Prophylaxis of cervical cancer and related cervical disease: a review of the cost-effectiveness of vaccination against oncogenic HPV types.J Manag Care Pharm. 2010 Apr;16(3):217-30. doi: 10.18553/jmcp.2010.16.3.217. J Manag Care Pharm. 2010. PMID: 20331326 Free PMC article. Review.
-
Human papillomavirus vaccination and the role of herd effects in future cancer control planning: a review.Expert Rev Vaccines. 2018 May;17(5):395-409. doi: 10.1080/14760584.2018.1471986. Epub 2018 May 21. Expert Rev Vaccines. 2018. PMID: 29715059 Review.
Cited by
-
Modelling and stability analysis of the dynamics of measles with application to Ethiopian data.Heliyon. 2024 Jul 2;10(13):e33594. doi: 10.1016/j.heliyon.2024.e33594. eCollection 2024 Jul 15. Heliyon. 2024. PMID: 39670224 Free PMC article.
-
Mathematical analysis of the dynamics of cyberattack propagation in IoT networks.PLoS One. 2025 May 16;20(5):e0322391. doi: 10.1371/journal.pone.0322391. eCollection 2025. PLoS One. 2025. PMID: 40378094 Free PMC article.
-
Analysis of vaccination strategies in a heterosexual HPV transmission model with a case study in Xinjiang of China.Infect Dis Model. 2025 Jun 23;10(4):1153-1178. doi: 10.1016/j.idm.2025.06.004. eCollection 2025 Dec. Infect Dis Model. 2025. PMID: 40678791 Free PMC article.
-
Assessing vaccine efficacy for infectious diseases with variable immunity using a mathematical model.Sci Rep. 2024 Aug 10;14(1):18572. doi: 10.1038/s41598-024-69651-6. Sci Rep. 2024. PMID: 39127773 Free PMC article.
-
Modelling and Analysis of the Epidemic Model under Pulse Charging in Wireless Rechargeable Sensor Networks.Entropy (Basel). 2021 Jul 21;23(8):927. doi: 10.3390/e23080927. Entropy (Basel). 2021. PMID: 34441067 Free PMC article.
References
-
- World Health Organization, human papillomavirus (hpv) and cervical cancer 2020. https://www.who.int/news-room/fact-sheets/detail/human-papillomavirus-(h... (2020)
-
- Lemos-Paiao AP, Silva CJ, Torres DF. An epidemic model for cholera with optimal control treatment. J. Comput. Appl. Math. 2017;318:168–180. doi: 10.1016/j.cam.2016.11.002. - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources
