Improved accuracy of cerebral blood flow quantification in the presence of systemic physiology cross-talk using multi-layer Monte Carlo modeling

Abstract

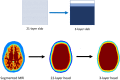
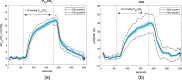
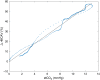
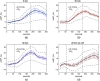
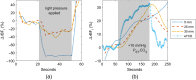
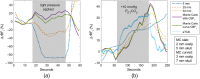
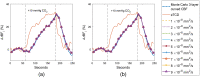
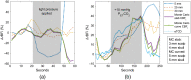
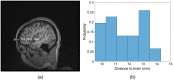
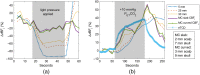
Significance: Contamination of diffuse correlation spectroscopy (DCS) measurements of cerebral blood flow (CBF) due to systemic physiology remains a significant challenge in the clinical translation of DCS for neuromonitoring. Tunable, multi-layer Monte Carlo-based (MC) light transport models have the potential to remove extracerebral flow cross-talk in cerebral blood flow index ( ${\mathrm{CBF}}_i$ ) estimates. Aim: We explore the effectiveness of MC DCS models in recovering accurate ${\mathrm{CBF}}_i$ changes in the presence of strong systemic physiology variations during a hypercapnia maneuver. Approach: Multi-layer slab and head-like realistic (curved) geometries were used to run MC simulations of photon propagation through the head. The simulation data were post-processed into models with variable extracerebral thicknesses and used to fit DCS multi-distance intensity autocorrelation measurements to estimate ${\mathrm{CBF}}_i$ timecourses. The results of the MC ${\mathrm{CBF}}_i$ values from a set of human subject hypercapnia sessions were compared with ${\mathrm{CBF}}_i$ values estimated using a semi-infinite analytical model, as commonly used in the field. Results: Group averages indicate a gradual systemic increase in blood flow following a different temporal profile versus the expected rapid CBF response. Optimized MC models, guided by several intrinsic criteria and a pressure modulation maneuver, were able to more effectively separate ${\mathrm{CBF}}_i$ changes from scalp blood flow influence than the analytical fitting, which assumed a homogeneous medium. Three-layer models performed better than two-layer ones; slab and curved models achieved largely similar results, though curved geometries were closer to physiological layer thicknesses. Conclusion: Three-layer, adjustable MC models can be useful in separating distinct changes in scalp and brain blood flow. Pressure modulation, along with reasonable estimates of physiological parameters, can help direct the choice of appropriate layer thicknesses in MC models.

Keywords: Monte Carlo; cerebral blood flow; diffuse correlation spectroscopy; hypercapnia; multi-layer.

Fig. 1

Top row: the 21-layer slab is concatenated into a 2-, 3-, or 4-layer volume in post-processing (3 layer is shown). Bottom row: the segmented MRI is iteratively image-eroded to make a 22-layer head volume and is analogously post-processed into a 2-, 3-, or 4-layer volume.

Fig. 2

Group averaged ${\mathrm{P}}_{\mathrm{ET}}{\mathrm{CO}}_2$ timecourse for all subjects with concurrent TCD measurements, with standard errors in light blue and the quartiles plotted in dotted lines (a), and the corresponding averaged TCD timecourse for the same subjects (b).

Fig. 3

Example $\mathrm{\Delta }\mathrm{TCD}$ timecourse plotted against its corresponding $\mathrm{\Delta }{\mathrm{P}}_{\mathrm{ET}}{\mathrm{CO}}_2$ timecourse. The linear regression fit is overlaid in blue.

Fig. 4

Group average of (a) 5-mm detector, (b) 25-mm detector, and (c) 30 mm detector, totaling 46 measurements. (d) A 28-measurement subset of those that contained a 20-mm probe on the subject calf. The error bars represent standard error, and the dotted timecourses above and below the group average represent the 25th and 75th quartiles, respectively.

Fig. 5

Analytical fitting-based timecourses of ΔrBFi of subject 1 during (a) pressure modulation with light pressure applied approximately between 20 and 50 s from the start, and (b) hypercapnia in terms of the percentage change in the baseline normalized $\mathrm{\Delta }{\mathrm{rBF}}_{\mathrm{i}}$. Shading indicates the pressure period for (a) and the ${\mathrm{CO}}_2$ enriched breathing gas delivery period for (b).

Fig. 6

Subject 1 hypercapnia timecourse fitted with (a) MC-2L slab model and (b) curved model overlaid with the analytical fit at 25- and 30-mm separations and eTCD. Only fitting results using MC models with up to 6-mm extracerebral thickness are shown.

Fig. 7

Subject 1 timecourses fitted with MC-3L slab and curved models overlaid with the analytical fit at 5-, 25-, and 30-mm separations and eTCD during (a) pressure modulation and (b) hypercapnia measurements.

Fig. 8

Monte Carlo slab and curved fits for subject 1 for (a) pressure modulation and (b) hypercapnia using variable scattering values across tissue layers.

Fig. 9

MC curved, four-layer fits with various diffusion coefficients used for the CSF layer for subject 1. A 1-mm CSF thickness was used for (a) and a 2-mm thickness was used for (b).

Fig. 10

Subject 2 timecourses fitted with MC-3L slab and curved models overlaid with the analytical fit at 5-, 25- and 30-mm separations and eTCD during (a) pressure modulation and (b) hypercapnia measurements.

Fig. 11

Total extracerebral thickness for subject 2 as measured using a distance ruler on image software (a) and a mesh-based MATLAB function after segmentation (b).

Fig. 12

Subject 3 timecourses fitted with MC-3L slab and curved models overlaid with the analytical fit at 5-, 25- and 30-mm separations and eTCD during (a) pressure modulation and (b) hypercapnia measurements.