Ultra-Stable Molecular Sensors by Sub-Micron Referencing and Why They Should Be Interrogated by Optical Diffraction-Part I. The Concept of a Spatial Affinity Lock-in Amplifier

Abstract

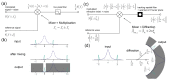
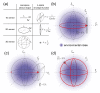
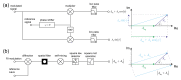
Label-free optical biosensors, such as surface plasmon resonance, are sensitive and well-established for the characterization of molecular interactions. Yet, these sensors require stabilization and constant conditions even with the use of reference channels. In this paper, we use tools from signal processing to show why these sensors are so cross-sensitive and how to overcome their drawbacks. In particular, we conceptualize the spatial affinity lock-in as a universal design principle for sensitive molecular sensors even in the complete absence of stabilization. The spatial affinity lock-in is analogous to the well-established time-domain lock-in. Instead of a time-domain signal, it modulates the binding signal at a high spatial frequency to separate it from the low spatial frequency environmental noise in Fourier space. In addition, direct sampling of the locked-in sensor's response in Fourier space enabled by diffraction has advantages over sampling in real space as done by surface plasmon resonance sensors using the distributed reference principle. This paper and part II hint at the potential of spatially locked-in diffractometric biosensors to surpass state-of-the-art temperature-stabilized refractometric biosensors. Even simple, miniaturized and non-stabilized sensors might achieve the performance of bulky lab instruments. This may enable new applications in label-free analysis of molecular binding and point-of-care diagnostics.

Keywords: chemosensors, biosensors; focal molography; lock-in amplifiers; molecular sensors; noise analysis; noise rejection; optical diffraction.

Figure A1

Schematic of a Fourier plane (red) in reciprocal space as it can be sampled by for instance an image detector that is placed at a Fourier plane of an optical system. The violet circle is the set of possible outgoing modes ${\overrightarrow{\beta }}_{\mathrm{out}}$ and the vector that is depicted fulfills the diffraction condition. The schematic is a slice of reciprocal space along the ${\xi }_x,{\xi }_z$ direction and must be imagined in 3D. Furthermore, equal momentum of incoming and outgoing mode were assumed, which is only the case if they propagate in media with equal refractive indices.

Figure 1

The spatial affinity lock-in concept. Environmental noise and signal distribution are shown for different sensor designs. In all cases, we assume a sensor that interrogates a volume close to its surface and detects changes in the refractive index within that volume. The second column shows the reciprocal space (also known as momentum or k-space) distribution of binding signal and environmental noise. (a) Typical environmental noise sources such as temperature gradients or non-specific binding of background molecules, are ‘long’ ranged. They usually exhibit a dominant correlation mechanism and display a Lorenzian shape in momentum space. (b) An integrative sensor with the analyte molecules bound uniformly has a spectral distribution of the signal centered around zero spatial frequency in reciprocal space where most of the environmental noise is situated. (c) A traditional referenced sensor still has most of the signal at DC and there is a significant spectral overlap between the two signal lobes because the modulation period is of similar size as the sensor dimension. (d) A locked-in sensor has a lock-in period that is much smaller than its lateral dimension. The signal lobes are clearly separated, and the signal is situated at spatial frequencies where there is hardly any environmental noise. As a remark, because we simply want to illustrate the concept, we have neglected a zero-frequency component that is because we cannot put a negative mass analyte molecule onto the reference. Also, we neglected all higher harmonics that are due to the rectangular distribution of biomolecular mass in this figure.

Figure 2

Analogies between a temporal (a,b) and a spatial lock-in (c,d) illustrated at simplified schematics a) The temporal lock-in uses a reference wave $\delta \left(f\pm f_1\right)$ from the same source as the signal (frequency $f_1$) that is mixed (multiplied) with the modulated and enveloped signal $S\left(f\pm f_1\right)$. This produces the sum and the difference of the two frequencies $f_1$ and locks one of the lobes of the signal to DC. A low-pass filter then isolates the DC component and produces an output that is proportional to the signal amplitude. (b) schematic depiction how the signal and the noise are shifted by the mixing and filtered by the low-pass filter. (c) In the spatial lock-in system a reference wave with momentum ${\overrightarrow{\beta }}_{\mathrm{in}}$ is mixed (diffracted) with the grating/crystal momentum of ordered matter (enveloped because of finite spatial extent $S\left(\overrightarrow{\xi }\pm {\overrightarrow{\xi }}_g\right)$) and produces two diffracted waves ${\overrightarrow{\beta }}_{\mathrm{out}}$. A spatial filter in a Fourier plane is then used to isolate one of these diffracted waves. (d) Schematic depiction how the modulated input and noise are mapped onto different angular directions by diffraction. The low frequency environmental noise is primarily scattered in the forward direction. A spatial filter isolates the signal component of interest.

Figure 3

Transfer functions of spatial lock-ins and schematic 1/$\xi$ (environmental) noise (a) Transfer functions of 1D, 2D and 3D sensors. The volume of the envelope function in reciprocal space decreases with increasing dimensionality of the sensor. For a given lock-in frequency, the amount of picked up noise decreases from 1D to 3D sensors. (b) 2D sensor transfer functions with equal signal-to-noise ratio and the same lock-in momentum magnitude $\left|\overrightarrow{\xi }\right|$ form a circle in the ${\xi }_x$, ${\xi }_y$ plane (c) 1D sensor transfer functions with equal SNR and the same lock-in momentum magnitude are just two points in reciprocal space. (d) 3D sensor transfer functions with the same SNR and same lock-in momentum represent an entire sphere in reciprocal space. This allows for many possible sensor realizations.

Figure 4

Advantages and disadvantages of digital and analog spatial lock-in amplifiers. Digital lock-in amplifiers such as surface plasmon resonance sensors using distributed referencing acquire the signal in real space whereas analog lock-in amplifiers (diffractometric sensor) sample directly reciprocal space. Due to this simple difference analog lock-in amplifiers have numerous advantages over digital lock-ins.

Figure 5

Difference between phase lock-in and pure frequency lock-in (a) A phase lock-in requires a reference signal with a fixed phase relationship to the signal. By mixing the signal with the reference and a 90${}^{\circ }$ shifted reference one can obtain the in-phase and quadrature components of the resulting phasor. This allows both magnitude and phase of the resultant to be determined. (b) A frequency lock-in such as a diffractometric biosensor loses the phase information because only the square magnitude of the resultant phasor can be detected (square law detection).