Privacy preserving data visualizations
- PMID: 33442528
- PMCID: PMC7790778
- DOI: 10.1140/epjds/s13688-020-00257-4
Privacy preserving data visualizations
Abstract
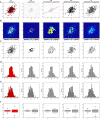
Data visualizations are a valuable tool used during both statistical analysis and the interpretation of results as they graphically reveal useful information about the structure, properties and relationships between variables, which may otherwise be concealed in tabulated data. In disciplines like medicine and the social sciences, where collected data include sensitive information about study participants, the sharing and publication of individual-level records is controlled by data protection laws and ethico-legal norms. Thus, as data visualizations - such as graphs and plots - may be linked to other released information and used to identify study participants and their personal attributes, their creation is often prohibited by the terms of data use. These restrictions are enforced to reduce the risk of breaching data subject confidentiality, however they limit analysts from displaying useful descriptive plots for their research features and findings. Here we propose the use of anonymization techniques to generate privacy-preserving visualizations that retain the statistical properties of the underlying data while still adhering to strict data disclosure rules. We demonstrate the use of (i) the well-known k-anonymization process which preserves privacy by reducing the granularity of the data using suppression and generalization, (ii) a novel deterministic approach that replaces individual-level observations with the centroids of each k nearest neighbours, and (iii) a probabilistic procedure that perturbs individual attributes with the addition of random stochastic noise. We apply the proposed methods to generate privacy-preserving data visualizations for exploratory data analysis and inferential regression plot diagnostics, and we discuss their strengths and limitations.
Keywords: Anonymization; Data visualizations; Disclosure control; Privacy protection; Sensitive data.
© The Author(s) 2020.
Conflict of interest statement
Competing interestsThe authors declare that they have no competing interests.
Figures







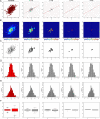





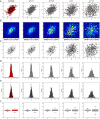
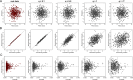


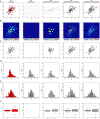


References
-
- O’Donoghue SI, Baldi BF, Clark SJ, Darling AE, Hogan JM, Kaur S, Maier-Hein L, McCarthy DJ, Moore WJ, Stenau E, Swedlow JR, Vuong J, Procter JB. Visualization of biomedical data. Annu Rev Biomed Data Sci. 2018;1(1):275–304. doi: 10.1146/annurev-biodatasci-080917-013424. - DOI
-
- Matejka J, Fitzmaurice G. Proceedings of the 2017 CHI conference on human factors in computing systems. New York: ACM; 2017. Same stats, different graphs: generating datasets with varied appearance and identical statistics through simulated annealing; pp. 1290–1294.
-
- Morrison J, Vogel D. The impacts of presentation visuals on persuasion. Inf Manag. 1998;33(3):125–135. doi: 10.1016/S0378-7206(97)00041-4. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
