Binary Amplitude Reflection Gratings for X-ray Shearing and Hartmann Wavefront Sensors

Abstract

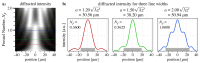
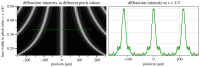
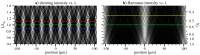
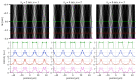
New, high-coherent-flux X-ray beamlines at synchrotron and free-electron laser light sources rely on wavefront sensors to achieve and maintain optimal alignment under dynamic operating conditions. This includes feedback to adaptive X-ray optics. We describe the design and modeling of a new class of binary-amplitude reflective gratings for shearing interferometry and Hartmann wavefront sensing. Compact arrays of deeply etched gratings illuminated at glancing incidence can withstand higher power densities than transmission membranes and can be designed to operate across a broad range of photon energies with a fixed grating-to-detector distance. Coherent wave-propagation is used to study the energy bandwidth of individual elements in an array and to set the design parameters. We observe that shearing operates well over a ±10% bandwidth, while Hartmann can be extended to ±30% or more, in our configuration. We apply this methodology to the design of a wavefront sensor for a soft X-ray beamline operating from 230 eV to 1400 eV and model shearing and Hartmann tests in the presence of varying wavefront aberration types and magnitudes.

Keywords: Hartmann; Talbot; X-ray; aberrations; grating; interferometry; shearing; wavefront.

Figure 1

(a) Beam geometry used in the single-grating shearing interferometry and Hartmann wavefront. A converging (shown) or diverging beam, incident from the left, is transmitted by a shearing grating or Hartmann grid and propagates a distance z to the detection plane. The grating-to-focus distance is R (negative in the diverging-beam case). Inset details show (b) shearing geometry with grating pitch d and (c) Hartmann geometry with grid pitch D and opening width a.

Figure 2

Diffracted intensity patterns from a range of isolated Hartmann-grid line widths calculated with respect to the Fresnel number, $N_F=a^2/4\lambda z^{\prime }$, with fixed wavelength, $\lambda =2\mathrm{n}\mathrm{m}$, detector distance, $z=0.3\mathrm{m}$, and incident beam radius, $R=4\mathrm{m}$. Note that $\sqrt{\lambda z^{\prime }}=25.469\mathsf{\mu }\mathrm{m}$. (a) Each row is calculated independently and normalized to its maximum value. Yellow curves show the line width, references to the horizontal axis. Red, green, and blue lines show the positions of three specific diffracted intensity calculations (b) extracted from the plot. Gray rectangles represent the line width in each case.

Figure 3

Coherent wave-propagation calculations of Hartmann grid diffraction intensity patterns as a function of the pitch, D. A constant line width, $a=38.203 \mathsf{\mu }\mathrm{m}$, is maintained (Equation (8)). The plot on the right shows three periods of the pattern, calculated at $r=1/3$, extracted at the position of the green line.

Figure 4

Coherent wave-propagation models of shearing and Hartmann detector-plane intensities for a range of wavelengths about ${\lambda }_0$ = 2 $\mathrm{n}$$\mathrm{m}$ (green line), in a converging beam. Each row is normalized for constant integrated power. Pitch values are $d=25.469 \mathsf{\mu }\mathrm{m}$ for shearing and $D=114.609 \mathsf{\mu }\mathrm{m}$ for Hartmann with $a=38.203 \mathsf{\mu }\mathrm{m}$. (a) Red and blue reference lines represent a $\pm 10\%$ wavelength change. (b) Hartmann calculations show separation between neighboring beamlets. The yellow line marks a +30% wavelength change, where $\beta$ = 0.690. The corresponding Fresnel number is shown at the right.

Figure 5

Coherent wave-propagation calculations of the detector-plane, central intensity region in shearing interferometry, for a 2, 4, and 6 $\mathrm{n}$$\mathrm{m}$ wavelength, with a fixed geometry matching Figure 4a. Eighty, uniformly-illuminated grating lines are modeled in each case. Conditions match the first three Talbot planes, respectively. Each row is normalized for constant integrated power. Green lines indicate the Talbot condition. Blue, red, and magenta lines show wavelength shifts of $-0.133$ $\mathrm{n}$$\mathrm{m}$, $-0.267$ $\mathrm{n}$$\mathrm{m}$, and $-0.400$ $\mathrm{n}$$\mathrm{m}$, respectively. Corresponding intensity profiles are extracted from the wavelength offsets and plotted below.

Figure 6

Illustration of the wavefront sensor grating array, its pattern, and use. (a) The narrow beam has a 2°, glancing angle of incidence and a longitudinal footprint longer than the array, so the four patterns in a column are illuminated at once. The inset grating cross-section detail shows how light reflects from the top surface, yet all other light is blocked by the thin walls and etched pattern features. At low angles, the detection-plane scintillator may be upright or inclined. The pattern (c) is etched into a silicon wafer chip (b), which is approximately 28 $\mathrm{m}$$\mathrm{m}$ wide. The pattern’s five columns contain 12 shearing gratings (Columns 1–3), four Hartmann grids (Column 4), and an open mirror region (column 5).

Figure 7

Design of shearing and Hartmann arrays spanning a 230 eV to 1400 eV energy range. (a) Counting 0 to 11, twelve gratings span the range with $\beta =0.1624$, using the first Talbot plane ($n=1$). Blue-colored regions show the individual gratings’ operating energy range. The equivalent energy range is shown for the second and third Talbot planes in green and red. (b) Corresponding grating pitch values. (c) With $\beta =0.4351$, four Hartmann grids (Numbered 0 to 3) span the range. (d) Corresponding Hartmann grid pitch values.

Figure 8

Modeled shearing detector-plane intensity patterns. The four gratings of Column 2 are illuminated with wavelengths shown above each detail. Grating pitch values are shown on the right. Square-wave intensity patterns are reproduced at the four design wavelengths (green markers), while the intermediate wavelength (red marker) shows that gratings from the two middle rows can both be used. The green colored rectangles align to the scale at the left and show the wavelength ranges over which each grating is designed to be used.

Figure 9

Hartmann detector-plane intensity pattern detail, calculated for the wavelength corresponding to the design of the second-lowest row (green marker). The beamlets in that row have a smooth intensity profile and minimal overlap. Green colored rectangles align to the scale at the left and show wavelength ranges over which each grid is designed to be used. We observe that the two grids designed for larger wavelengths project spots with a more prominent structure, while grids designed for smaller wavelengths show adjacent beamlet interference.

Figure 10

(a) Shearing and (b) Hartmann aberration modeling showing four different aberration types and varying amplitudes. Each row is a detail extracted from an intensity calculation performed for a single grating or grid on a 2 $\mathrm{m}$$\mathrm{m}$ wide domain. The scale bars on the left show the uniformly-weighted aberration rms amplitudes for the polynomials and the peak height for the Gaussian cases.