WASP: a software package for correctly characterizing the topological development of ribbon structures
- PMID: 33452342
- PMCID: PMC7811023
- DOI: 10.1038/s41598-020-80851-8
WASP: a software package for correctly characterizing the topological development of ribbon structures
Abstract
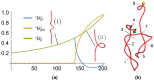
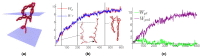
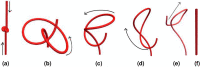
We introduce the Writhe Application Software Package (WASP) which can be used to characterisze the topology of ribbon structures, the underlying mathematical model of DNA, Biopolymers, superfluid vorticies, elastic ropes and magnetic flux ropes. This characterization is achieved by the general twist-writhe decomposition of both open and closed ribbons, in particular through a quantity termed the polar writhe. We demonstrate how this decomposition is far more natural and straightforward than artificial closure methods commonly utilized in DNA modelling. In particular, we demonstrate how the decomposition of the polar writhe into local and non-local components distinctly characterizes the local helical structure and knotting/linking of the ribbon. This decomposition provides additional information not given by alternative approaches. As example applications, the WASP routines are used to characterise the evolving topology (writhe) of DNA minicircle and open ended plectoneme formation magnetic/optical tweezer simulations, and it is shown that the decomponsition into local and non-local components is particularly important for the detection of plectonemes. Finally it is demonstrated that a number of well known alternative writhe expressions are actually simplifications of the polar writhe measure.
Conflict of interest statement
The authors declare no competing interests.
Figures
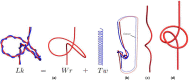








References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

