Probabilistic Models with Deep Neural Networks
- PMID: 33477544
- PMCID: PMC7831091
- DOI: 10.3390/e23010117
Probabilistic Models with Deep Neural Networks
Abstract
Recent advances in statistical inference have significantly expanded the toolbox of probabilistic modeling. Historically, probabilistic modeling has been constrained to very restricted model classes, where exact or approximate probabilistic inference is feasible. However, developments in variational inference, a general form of approximate probabilistic inference that originated in statistical physics, have enabled probabilistic modeling to overcome these limitations: (i) Approximate probabilistic inference is now possible over a broad class of probabilistic models containing a large number of parameters, and (ii) scalable inference methods based on stochastic gradient descent and distributed computing engines allow probabilistic modeling to be applied to massive data sets. One important practical consequence of these advances is the possibility to include deep neural networks within probabilistic models, thereby capturing complex non-linear stochastic relationships between the random variables. These advances, in conjunction with the release of novel probabilistic modeling toolboxes, have greatly expanded the scope of applications of probabilistic models, and allowed the models to take advantage of the recent strides made by the deep learning community. In this paper, we provide an overview of the main concepts, methods, and tools needed to use deep neural networks within a probabilistic modeling framework.
Keywords: Bayesian learning; deep probabilistic modeling; latent variable models; neural networks; variational inference.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
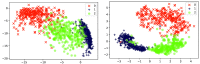
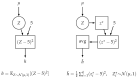
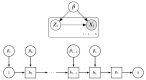
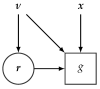
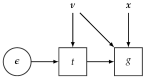
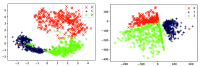
References
-
- Pearl J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann Publishers; San Mateo, CA, USA: 1988.
-
- Lauritzen S.L. Propagation of probabilities, means, and variances in mixed graphical association models. J. Am. Stat. Assoc. 1992;87:1098–1108. doi: 10.1080/01621459.1992.10476265. - DOI
-
- Russell S.J., Norvig P. Artificial Intelligence: A Modern Approach. Pearson; Upper Saddle River, NJ, USA: 2016.
-
- Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. Springer; Berlin/Heidelberg, Germany: 2001.
-
- Bishop C.M. Pattern Recognition and Machine Learning. Springer; Berlin/Heidelberg, Germany: 2006.
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

