Estimating a Stoichiometric Solid's Gibbs Free Energy Model by Means of a Constrained Evolutionary Strategy

Abstract

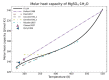
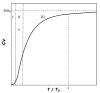
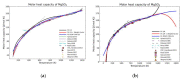
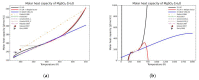
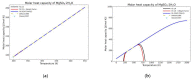
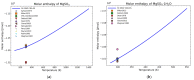
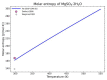
Modeling of thermodynamic properties, like heat capacities for stoichiometric solids, includes the treatment of different sources of data which may be inconsistent and diverse. In this work, an approach based on the covariance matrix adaptation evolution strategy (CMA-ES) is proposed and described as an alternative method for data treatment and fitting with the support of data source dependent weight factors and physical constraints. This is applied to a Gibb's Free Energy stoichiometric model for different magnesium sulfate hydrates by means of the NASA9 polynomial. Its behavior is proved by: (i) The comparison of the model to other standard methods for different heat capacity data, yielding a more plausible curve at high temperature ranges; (ii) the comparison of the fitted heat capacity values of MgSO₄·7H₂O against DSC measurements, resulting in a mean relative error of a 0.7% and a normalized root mean square deviation of 1.1%; and (iii) comparing the Van't Hoff and proposed Stoichiometric model vapor-solid equilibrium curves to different literature data for MgSO₄·7H₂O, MgSO₄·6H₂O, and MgSO₄·1H₂O, resulting in similar equilibrium values, especially for MgSO₄·7H₂O and MgSO₄·6H₂O. The results show good agreement with the employed data and confirm this method as a viable alternative for fitting complex physically constrained data sets, while being a potential approach for automatic data fitting of substance data.

Keywords: NASA9; constrained evolutionary strategy; data dispersion; data fitting; heat capacity; magnesium sulfate; salt hydrates; stoichiometric solid model; thermodynamic model; vapor-solid equilibrium.

Figure 1

Fitting of the heat capacity for the substance MgSO₄·1H₂O using the Levenberg-Marquardt algorithm.

Figure 2

Comparison of fit results from a standard LM-algorithm and the addition of weight factors (red) for: (a) Anhydrous magnesium sulfate; (b) magnesium sulfate monohydrate.

Figure 3

Example of two-dimensional spherical optimization problem. Points are individuals, the blue area is the solution area, and the dashed line is the dispersion calculated with the covariance matrix. Generation 1 shows the initial random distribution. Generations 2–3 show the population moving towards the detected favorable direction of the solution due to the ranking of the individuals. Higher random dispersion is expected as the algorithm looks for other possible minima in the vicinity by “mutation”. In generations 4–6, after the individuals are sufficiently dispersed, with the information of the covariance matrix, the global minimum is pinpointed and all the individuals, regardless of their initial position, converge to the final solution area.

Figure 4

Qualitative curve of the Debye model, the three regions indicate the application of the different established conditions.

Figure 5

Comparison of the different fit results of MgSO₄ showing: (a) literature points region; (b) extended range until 2000 K.

Figure 6

Comparison of the different fit results of MgSO₄·1H₂O showing: (a) literature points region; (b) extended range until 2000 K.

Figure 7

Comparison of the different fit results of MgSO₄·2H₂O showing: (a) literature points region; (b) extended range until 2000 K.

Figure 8

Comparison of the different fit results of MgSO₄·4H₂O showing: (a) literature points region; (b) extended range until 2000 K.

Figure 9

Comparison of the different fit results of MgSO₄·5H₂O showing: (a) literature points region; (b) extended range until 2000 K.

Figure 10

Comparison of the different fit results of MgSO₄·6H₂O showing: (a) literature points area; (b) extended range until 2000 K.

Figure 11

Comparison of the different fit results of MgSO₄·7H₂O showing: (a) literature points region; (b) extended range until 2000 K.

Figure 12

Comparison of the different fit results, showing the literature data in green (mean of the values) with the 95% confidence interval boundaries of: (a) MgSO₄; (b) MgSO₄·1H₂O.

Figure 13

Comparison of the different fit results, showing the literature data in green (mean of the values) with the 95% confidence interval boundaries of: (a) MgSO₄·2H₂O; (b) MgSO₄·4H₂O.

Figure 14

Comparison of the different fit results, showing the literature data in green (mean of the values) with the 95% confidence interval boundaries of: (a) MgSO₄·6H₂O; (b) MgSO₄·7H₂O.

Figure 15

Fitted results of the enthalpy curve in the literature points region for: (a) MgSO₄; (b) MgSO₄·1H₂O.

Figure 16

Fitted results of the entropy curve in the literature points region for: (a) MgSO₄; (b) MgSO₄·1H₂O.

Figure 17

Fitted results of the entropy curve in the literature points region for MgSO₄·2H₂O.

Figure 18

Comparison between the fitted heat capacity with the CMA-ES method and the experimental output from the DSC setup.

Figure 19

Temperature—vapor pressure comparison of MgSO₄·7H₂O between experimental data from Steiger et al. [37], Van’t Hoff curves, and the calculation of this work taking the MgSO₄·7H₂O as the fixed composition (black lines): (a) for a limited range to show literature points for the dehydration of MgSO₄·7H₂O and MgSO₄·6H₂O; (b) extended range to show further curves and the dehydration of MgSO₄·1H₂O.