Laboratory earthquake forecasting: A machine learning competition

Abstract

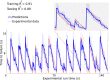
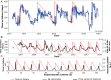
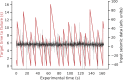
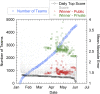
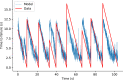
Earthquake prediction, the long-sought holy grail of earthquake science, continues to confound Earth scientists. Could we make advances by crowdsourcing, drawing from the vast knowledge and creativity of the machine learning (ML) community? We used Google's ML competition platform, Kaggle, to engage the worldwide ML community with a competition to develop and improve data analysis approaches on a forecasting problem that uses laboratory earthquake data. The competitors were tasked with predicting the time remaining before the next earthquake of successive laboratory quake events, based on only a small portion of the laboratory seismic data. The more than 4,500 participating teams created and shared more than 400 computer programs in openly accessible notebooks. Complementing the now well-known features of seismic data that map to fault criticality in the laboratory, the winning teams employed unexpected strategies based on rescaling failure times as a fraction of the seismic cycle and comparing input distribution of training and testing data. In addition to yielding scientific insights into fault processes in the laboratory and their relation with the evolution of the statistical properties of the associated seismic data, the competition serves as a pedagogical tool for teaching ML in geophysics. The approach may provide a model for other competitions in geosciences or other domains of study to help engage the ML community on problems of significance.

Keywords: earthquake prediction; laboratory earthquakes; machine learning competition; physics of faulting.

Fig. 1.

Experimental configuration and data collected. The biaxial experiment shear configuration and data collected. (Upper Left) The experiment is composed of three steel blocks with fault gouge contained within two shear zones. The fault gouge is composed of glass beads with dimensions on the order of 120 μm and a layer thickness of 4 mm for each fault. The configuration is held in place by a fixed horizontal (normal) load of 5 MPa. The central block is driven downward at a constant velocity. Acoustic emission is recorded by a lead zirconate titanate (PZT) piezoelectric ceramic transducer. (Upper Right) Measured shear stress as a function of experimental run time. There is a run-in displacement during which the shear stress increases until the gouge material begins to stick–slip quasiperiodically. This occurs for roughly half the experiment, followed by the central block failing intermittently and then sliding stably. Lower Left and Lower Right show expanded views of the acoustic emission signal and shear stress signal, respectively, for the shaded region in the shear stress signal, where the laboratory quakes are relatively periodic. arb., arbitrary. Reprinted with permission from ref. .

Fig. 2.

Random forest (RF) approach for predicting time remaining before failure. Failure times are determined by the large stress drops associated with the laboratory earthquakes, as seen in Fig. 1, Lower Right. The RF prediction (blue line) is shown on the testing data (data not previously seen by the ML algorithm) with 90$\%$ CIs (blue shaded region). The predictions agree very well with the actual remaining times before failure (red curve). The testing data are entirely independent of the training data and were not used to construct the model. Inset shows an expanded view of three slip cycles, illustrating that the trained model does well on aperiodic slip events (data are from laboratory experiment no. p2394 at Penn State). Reprinted with permission from ref. .

Fig. 3.

Subduction in Cascadia. Cross-sectional view of the Cascadia subduction zone in the region of Vancouver Island. Arrows indicate the sense of motion of the subducting Jan de Fuca plate beneath the North American plate. Adapted from ref. , which is licensed under CC BY 4.0.

Fig. 4.

Slow slip time to failure estimates, seismic features identified by the ML model, and comparison with laboratory experiments. (A) Testing set ML estimates of time to failure (blue) and measured time to failure of slow earthquakes in Cascadia, in the region of Vancouver Island. CC, correlation coefficient. (B) The most important statistical feature of the seismic data is related to seismic signal energy (black curve). The seismic feature shows systematic patterns evolving through the slip cycle in relation to the timing of the succeeding slow earthquake in Cascadia (left axis). (The feature IQ60-40 range is the interquantile obtained by subtracting the 60th percentile from the 40th percentile.) (C) For comparison, the most important statistical feature found in laboratory slow slip experiments is acoustic power, which is proportional to signal energy (right-hand vertical axis). The similarity of the two measures, one in Earth and the other in the laboratory, suggests that the slip processes at both scales are related. Adapted from ref. , which is licensed under CC BY 4.0.

Fig. 5.

Competition training data. The black curve shows the seismic signal recorded on a piezoceramic transducer located on the biaxial apparatus side block (apparatus is shown in Fig. 1). Each burst in amplitude corresponds to a laboratory earthquake. The red curve shows the time to failure derived from the earthquakes and the measured shear stress on the experimental apparatus (as in Fig. 1). Competitors were tasked with predicting the time before the next laboratory quake only based on a small snapshot of seismic data.

Fig. 6.

Evolution of MAE scores. The number of teams (light blue squares) and the value of the MAE of the daily first place team on the validation set (black circles) over the period of the competition as determined on the public validation set until early June and finally determined on the private test set for the final ranking (hence the jump in MAE for the final evaluation). The gray dots represent MAE values for all other submissions on each day. The public (red circles; validation set) and private (green squares; testing set) MAEs for the winning team are shown for the winning team's submissions.

Fig. 7.

Comparison of the change in rank for the top five competitors on the last day of submission with that of the top five winners. Tables provide the rank, MAE, and total number of submissions for the top five competitors on the last day and for the winners.

Fig. 8.

Winning model of the competition, by Team Zoo, on the test set. Red indicates time remaining before the next laboratory earthquake, as the experimental time progresses. Blue indicates predictions of Team Zoo’s winning model (an ensemble model of gradient-boosted trees and neural networks) based on small snapshots of seismic data (https://www.kaggle.com/dkaraflos/1-geomean-nn-and-6featlgbm-2-259-private-lb has additional details).

Fig. 9.

Distribution of MAE for all of the teams. Model performance of all of the competing teams on the two test sets (public and private). The performance dropped on the private set, a telltale of overfitting.