Predictive Models for the Binary Diffusion Coefficient at Infinite Dilution in Polar and Nonpolar Fluids

Abstract

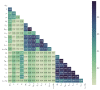
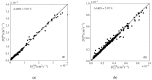
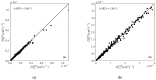
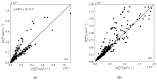
Experimental diffusivities are scarcely available, though their knowledge is essential to model rate-controlled processes. In this work various machine learning models to estimate diffusivities in polar and nonpolar solvents (except water and supercritical CO₂) were developed. Such models were trained on a database of 90 polar systems (1431 points) and 154 nonpolar systems (1129 points) with data on 20 properties. Five machine learning algorithms were evaluated: multilinear regression, k-nearest neighbors, decision tree, and two ensemble methods (random forest and gradient boosted). For both polar and nonpolar data, the best results were found using the gradient boosted algorithm. The model for polar systems contains 6 variables/parameters (temperature, solvent viscosity, solute molar mass, solute critical pressure, solvent molar mass, and solvent Lennard-Jones energy constant) and showed an average deviation (AARD) of 5.07%. The nonpolar model requires five variables/parameters (the same of polar systems except the Lennard-Jones constant) and presents AARD = 5.86%. These results were compared with four classic models, including the 2-parameter correlation of Magalhães et al. (AARD = 5.19/6.19% for polar/nonpolar) and the predictive Wilke-Chang equation (AARD = 40.92/29.19%). Nonetheless Magalhães et al. requires two parameters per system that must be previously fitted to data. The developed models are coded and provided as command line program.

Keywords: diffusion coefficient; machine learning; modeling; nonpolar; polar; prediction.

Figure 1

Correlation heat map for all properties and variables in the database of polar compounds. Colormap shows the absolute value of the Pearson correlation from zero (light green) to one (dark blue).

Figure 2

Correlation heat map for all properties and variables in the database of nonpolar compounds. Colormap shows the absolute value of the Pearson correlation from zero (light green) to one (dark blue).

Figure 3

Predicted versus experimental diffusivities for the test set of polar systems for the best machine learning model (Gradient Boosted): (a) plot including all calculated results; (b) plot zooming on lower $D_{12}$ range.

Figure 4

Predicted versus experimental diffusivities for the test set of nonpolar systems for the best machine learning model (Gradient Boosted) showing (a) plot including all calculated results; (b) plot zooming on lower $D_{12}$ range.

Figure 5

Calculated versus experimental diffusivities for the test set of polar systems for: (a) and (b) Wilke-Chang (Equation (1)) [5] and (c) and (d) Magalhães et al. (Equation (4)) [9] models. Note the distinct scale between plots.

Figure 5

Calculated versus experimental diffusivities for the test set of polar systems for: (a) and (b) Wilke-Chang (Equation (1)) [5] and (c) and (d) Magalhães et al. (Equation (4)) [9] models. Note the distinct scale between plots.

Figure 6

Calculated versus experimental diffusivities for the test set of nonpolar systems for: (a) and (b) Wilke-Chang (Equation (1)) [5] and (c) and (d) Magalhães et al. (Equation (4)) [9] models. Note the distinct scale between plots.

Figure 6

Calculated versus experimental diffusivities for the test set of nonpolar systems for: (a) and (b) Wilke-Chang (Equation (1)) [5] and (c) and (d) Magalhães et al. (Equation (4)) [9] models. Note the distinct scale between plots.