Model Reference Predictive Adaptive Control for Large-Scale Soft Robots

Abstract

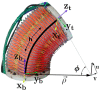
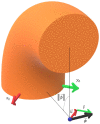
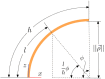
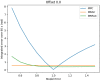
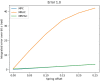
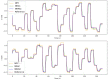
Past work has shown model predictive control (MPC) to be an effective strategy for controlling continuum joint soft robots using basic lumped-parameter models. However, the inaccuracies of these models often mean that an integral control scheme must be combined with MPC. In this paper we present a novel dynamic model formulation for continuum joint soft robots that is more accurate than previous models yet remains tractable for fast MPC. This model is based on a piecewise constant curvature (PCC) assumption and a relatively new kinematic representation that allows for computationally efficient state prediction. However, due to the difficulty in determining model parameters (e.g., inertias, damping, and spring effects) as well as effects common in continuum joint soft robots (hysteresis, complex pressure dynamics, etc.), we submit that regardless of the model selected, most model-based controllers of continuum joint soft robots would benefit from online model adaptation. Therefore, in this paper we also present a form of adaptive model predictive control based on model reference adaptive control (MRAC). We show that like MRAC, model reference predictive adaptive control (MRPAC) is able to compensate for "parameter mismatch" such as unknown inertia values. Our experiments also show that like MPC, MRPAC is robust to "structure mismatch" such as unmodeled disturbance forces not represented in the form of the adaptive regressor model. Experiments in simulation and hardware show that MRPAC outperforms individual MPC and MRAC.

Keywords: MRAC; adaptive control; continuum robot; dynamic modeling; model predictive control; parameter mismatch; soft robot; structure mismatch.

Figure 1

A continuum joint robot such as the one used for this work. The variables $\overrightarrow{\rho }$, ϕ, u, v, and h are labeled for reference.

Figure 2

A 3D schematic to illustrate the kinematic relationships used in the presented model derivation. $\overrightarrow{\varphi }$ is the axis-angle vector which can be decomposed into components parallel with the base frame b. Note that $\overrightarrow{u}$ points in the negative x_b direction and that $\overrightarrow{v}$ points in the positive y_b direction. The magnitude of the axis-angle vector $\overrightarrow{\varphi }$ is also the total bend angle.

Figure 3

A side view of the kinematic model of a continuum joint showing trigonometric relationships between variables.

Figure 4

Tracking error sensitivity to model error for all three controllers in simulation.

Figure 5

Joint trajectory tracking using all three controllers in simulation. This is for the case of errors in the model parameters used for MPC and MRPAC. Note that the reference trajectory corresponds to q_ref, the position states of our dynamic reference system defined in Equation (36). Also note that the performance of MRAC and MRPAC is indistinguishable.

Figure 6

Simulated tracking error sensitivity to unmodeled offset forces/torques (structure mismatch) if the rest of the model is perfect.

Figure 7

Simulated joint trajectory tracking of all three controllers with a perfect model besides an unmodeled offset torque. Note that the reference trajectory corresponds to q_ref, the position states of our dynamic reference system defined in Equation (36). Also note that the performance of MPC and MRPAC is indistinguishable.

Figure 8

Simulated joint trajectory tracking error as a function of both model parameter error (parameter mismatch) and a spring offset error (structure mismatch).

Figure 9

Joint trajectory tracking of all three controllers in hardware. Note that the reference trajectory corresponds to q_ref, the position states of our dynamic reference system defined in Equation (36).