Identifying Ultra Low Frequency Waves in the Lunar Plasma Environment Using Trajectory Analysisand Resonance Conditions
- PMID: 33505827
- PMCID: PMC7837453
- DOI: 10.1002/2017ja024018
Identifying Ultra Low Frequency Waves in the Lunar Plasma Environment Using Trajectory Analysisand Resonance Conditions
Abstract
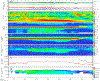
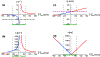
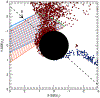
Recent studies show that localized crustal magnetic fields on the lunar surface can reflect a significant portion of the incoming solar wind protons. These reflected ions can drive a wide range of plasma waves. It is difficult to determine the intrinsic properties of low-frequency waves with single-spacecraft observations, which can be heavily Doppler shifted. We describe a technique to combine trajectory analysis of reflected protons with the Doppler shift and resonance conditions to identify ultralow-frequency waves at the Moon. On 31 January 2014 plasma waves were detected by one of the Acceleration, Reconnection, Turbulence and Electrodynamics of the Moon's Interaction with the Sun (ARTEMIS) probes as it approached the lunar wake; these waves were not detected by the second ARTEMIS probe located upstream in the undisturbed solar wind. The observed waves had a frequency below the local ion cyclotron frequency and had right-hand circular polarization in the reference frame of the Moon. By solving the Doppler shift and the cyclotron resonance equations, we determined the conditions for reflected ions to excite the observed waves. Simulated trajectories of reflected ions correspond to ARTEMIS ion observations and support the hypothesis that reflected ions are the primary driver of the waves. By combining trajectory analysis with the resonance conditions, we identify scenarios where ions that satisfy the resonance conditions are present in the right location to generate the observed waves. Using this method, we can uniquely identify the observed waves as upstream propagating right-hand polarized waves, subject to the assumption that they are generated by cyclotron resonance with ions.
Figures

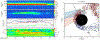

References
-
- Angelopoulos V (2011). The ARTEMIS mission. Space Science Review, 165, 3–25. 10.1007/s11214-010-9687-2 - DOI
-
- Auster HU, Glassmeier KH, Magnes W, Aydogar O, Baumjohann W, Constantinescu D, … Wiedemann M (2008). The THEMIS fluxgate magnetometer. Space Science Review, 141, 235–264. 10.1007/s11214-008-9365-9 - DOI
-
- Gurnett DA, & Bhattacharjee A (2005). Introduction to plasma physics: With space and laboratory applications. Cambridge, UK: Cambridge University Press.
-
- Halekas JS, Brain DA, Mitchell DL, & Lin RP (2006). Whistler waves observed near lunar crustal magnetic sources. Geophysical Research Letters, 33, L22104 10.1029/2006GL027684 - DOI
-
- Halekas JS, Poppe AR, Farrell WM, Delory GT, Angelopoulos V, McFadden JP, … Ergun RE (2012). Lunar precursor effects in the solar wind and terrestrial magnetosphere. Journal of Geophysical Research, 117, A05101 10.1029/2011JA017289 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
