Mathematical modeling for the outbreak of the coronavirus (COVID-19) under fractional nonlocal operator

Abstract

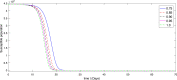
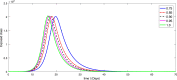
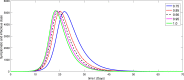
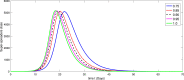
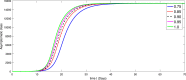
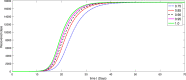
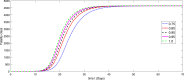
A mathematical model for the spread of the COVID-19 disease based on a fractional Atangana-Baleanu operator is studied. Some fixed point theorems and generalized Gronwall inequality through the AB fractional integral are applied to obtain the existence and stability results. The fractional Adams-Bashforth is used to discuss the corresponding numerical results. A numerical simulation is presented to show the behavior of the approximate solution in terms of graphs of the spread of COVID-19 in the Chinese city of Wuhan. We simulate our table for the data of Wuhan from February 15, 2020 to April 25, 2020 for 70 days. Finally, we present a debate about the followed simulation in characterizing how the transmission dynamics of infection can take place in society.

Keywords: Adams–Bashforth technique; Atangana–Baleanu operator; COVID-19; Fixed point technique; Generalized Gronwall inequality; Stability and existence theory.

Fig. 1

Dynamical behavior of $\mathbb{S}$ class of model (3) at various values of fractional order $q$.

Fig. 2

Dynamical behavior of $\mathbb{E}$ class of model (3) at various values of fractional order $q$.

Fig. 3

Dynamical behavior of $\mathbb{I}$ class of model (3) at various values of fractional order $q$.

Fig. 4

Dynamical behavior of $\mathbb{P}$ class of model (3) at various values of fractional order $q$.

Fig. 5

Dynamical behavior of $\mathbb{A}$ class of model (3) at various values of fractional order $q$.

Fig. 6

Dynamical behavior of $\mathbb{H}$ class of model (3) at various values of fractional order $q$.

Fig. 7

Dynamical behavior of $\mathbb{R}$ class of model (3) at various values of fractional order $q$.

Fig. 8

Dynamical behavior of $\mathbb{F}$ class of model (3) at various values of fractional order $q$.