Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Dec:19:103610.
doi: 10.1016/j.rinp.2020.103610. Epub 2020 Nov 16.

Mathematical modeling for the outbreak of the coronavirus (COVID-19) under fractional nonlocal operator

Saleh S Redhwan  1 , Mohammed S Abdo  2 , Kamal Shah  3 , Thabet Abdeljawad  4   5   6 , S Dawood  2 , Hakim A Abdo  7 , Sadikali L Shaikh  8
Affiliations

Mathematical modeling for the outbreak of the coronavirus (COVID-19) under fractional nonlocal operator

Saleh S Redhwan et al. Results Phys. 2020 Dec.

Abstract

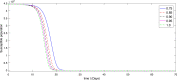
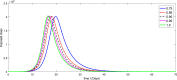
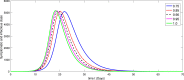
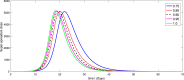
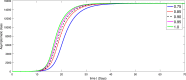
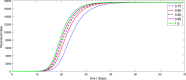
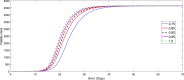
A mathematical model for the spread of the COVID-19 disease based on a fractional Atangana-Baleanu operator is studied. Some fixed point theorems and generalized Gronwall inequality through the AB fractional integral are applied to obtain the existence and stability results. The fractional Adams-Bashforth is used to discuss the corresponding numerical results. A numerical simulation is presented to show the behavior of the approximate solution in terms of graphs of the spread of COVID-19 in the Chinese city of Wuhan. We simulate our table for the data of Wuhan from February 15, 2020 to April 25, 2020 for 70 days. Finally, we present a debate about the followed simulation in characterizing how the transmission dynamics of infection can take place in society.

Keywords: Adams–Bashforth technique; Atangana–Baleanu operator; COVID-19; Fixed point technique; Generalized Gronwall inequality; Stability and existence theory.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Fig. 1
Fig. 1
Dynamical behavior of S class of model (3) at various values of fractional order q.
Fig. 2
Fig. 2
Dynamical behavior of E class of model (3) at various values of fractional order q.
Fig. 3
Fig. 3
Dynamical behavior of I class of model (3) at various values of fractional order q.
Fig. 4
Fig. 4
Dynamical behavior of P class of model (3) at various values of fractional order q.
Fig. 5
Fig. 5
Dynamical behavior of A class of model (3) at various values of fractional order q.
Fig. 6
Fig. 6
Dynamical behavior of H class of model (3) at various values of fractional order q.
Fig. 7
Fig. 7
Dynamical behavior of R class of model (3) at various values of fractional order q.
Fig. 8
Fig. 8
Dynamical behavior of F class of model (3) at various values of fractional order q.
See this image and copyright information in PMC

References

    1. Rachah A., Torres D.F.M. Dynamics and optimal control of Ebola transmission. Math Comput Sci. 2016;10:331–342. doi: 10.1007/s11786-016-0268-y. - DOI
    1. Kahn J.S., McIntosh K. History and recent advances in coronavirus discovery. Pediatric Infect Dis J. 2005;24(11):223–227. - PubMed
    1. Tyrrell D.A., Bynoe M.L. Cultivation of viruses from a high proportion ofpatients with colds. Lancet. 1966;1:76–77. - PubMed
    1. Ndaïrou F., Area I., Nieto J.J., Silva C.J., Torres D.F.M. Mathematical modeling of zika disease in pregnant women and newborns with microcephaly in Brazil. Math Methods Appl Sci. 2018;41:8929–8941.
    1. Brauer F., Castillo-Chavez C., Feng Z. Springer-Verlag New York; 2019. Mathematical Models in Epidemiology.

Further Reading

    1. Djordjevic J., Silva C.J., Torres D.F.M. A stochastic sica epidemic model for hiv transmission. Appl Math Lett. 2018;84:168–175. doi: 10.1016/j.aml.2018.05.005. - DOI

LinkOut - more resources