Numerical simulation and stability analysis for the fractional-order dynamics of COVID-19

Abstract

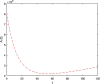
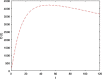
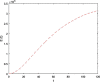
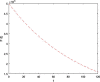
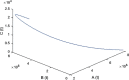
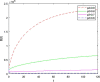
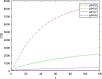
The main purpose of this work is to study the dynamics of a fractional-order Covid-19 model. An efficient computational method, which is based on the discretization of the domain and memory principle, is proposed to solve this fractional-order corona model numerically and the stability of the proposed method is also discussed. Efficiency of the proposed method is shown by listing the CPU time. It is shown that this method will work also for long-time behaviour. Numerical results and illustrative graphical simulation are given. The proposed discretization technique involves low computational cost.

Keywords: Corona virus model; Fractional derivatives; Stability analysis.

Fig. 1

Performance of group $(A)$ with time.

Fig. 2

Performance of group $(B)$ with time.

Fig. 3

Performance of group $(C)$ with time.

Fig. 4

Performance of group $(D)$ with time.

Fig. 5

Performance of group $(E)$ with time.

Fig. 6

Performance of group $(F)$ with time.

Fig. 7

Performance of groups $A(t)$, $B(t)$ and $C(t)$ for integer order relaxation.

Fig. 8

Performance of groups $B(t)$, $C(t)$ and $D(t)$ for integer order relaxation.

Fig. 9

Performance of groups $A(t)$, $B(t)$ and $E(t)$ for integer order relaxation.

Fig. 10

Performance of group $A(t)$ with time at distinct fractional values of time-derivatives.

Fig. 11

Performance of group $B(t)$ with time at distinct fractional values of time-derivatives.

Fig. 12

Performance of group $C(t)$ with time at distinct fractional values of time-derivatives.

Fig. 13

Performance of group $D(t)$ with time at distinct fractional values of time-derivatives.

Fig. 14

Performance of group $E(t)$ with time at distinct fractional values of time-derivatives.

Fig. 15

Performance of group $F(t)$ with time at distinct fractional values of time-derivatives.