Interpreting Interaction Effects in Generalized Linear Models of Nonlinear Probabilities and Counts
- PMID: 33523708
- PMCID: PMC8325704
- DOI: 10.1080/00273171.2020.1868966
Interpreting Interaction Effects in Generalized Linear Models of Nonlinear Probabilities and Counts
Abstract
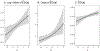
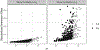
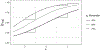
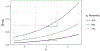
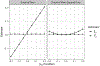
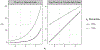
Psychology research frequently involves the study of probabilities and counts. These are typically analyzed using generalized linear models (GLMs), which can produce these quantities via nonlinear transformation of model parameters. Interactions are central within many research applications of these models. To date, typical practice in evaluating interactions for probabilities or counts extends directly from linear approaches, in which evidence of an interaction effect is supported by using the product term coefficient between variables of interest. However, unlike linear models, interaction effects in GLMs describing probabilities and counts are not equal to product terms between predictor variables. Instead, interactions may be functions of the predictors of a model, requiring nontraditional approaches for interpreting these effects accurately. Here, we define interactions as change in a marginal effect of one variable as a function of change in another variable, and describe the use of partial derivatives and discrete differences for quantifying these effects. Using guidelines and simulated examples, we then use these approaches to describe how interaction effects should be estimated and interpreted for GLMs on probability and count scales. We conclude with an example using the Adolescent Brain Cognitive Development Study demonstrating how to correctly evaluate interaction effects in a logistic model.
Keywords: Generalized linear modeling; Poisson; interaction; logistic regression; moderation.
Conflict of interest statement
Figures
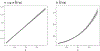


References
-
- Agresti A (2002). Categorical data analysis. Wiley. 10.1002/0471249688 - DOI
-
- Ai C, & Norton EC (2003). Interaction terms in logit and probit models. Economics Letters, 80(1), 123–129. 10.1016/S0165-1765(03)00032-6 - DOI
-
- Aiken LS, & West SG (1991). Multiple regression: Testing and interpreting interactions. Sage.
-
- Armstrong D (2020). DAMisc: Dave Armstrong’s miscellaneous functions. R package version 1.5.4. https://CRAN.R-project.org/package=DAMisc
MeSH terms
Grants and funding
- U24 DA041147/DA/NIDA NIH HHS/United States
- U01 DA041120/DA/NIDA NIH HHS/United States
- U01 DA041093/DA/NIDA NIH HHS/United States
- R01 DA047247/DA/NIDA NIH HHS/United States
- U24 DA041123/DA/NIDA NIH HHS/United States
- U01 DA041025/DA/NIDA NIH HHS/United States
- U01 DA041117/DA/NIDA NIH HHS/United States
- U01 DA041148/DA/NIDA NIH HHS/United States
- U01 DA041174/DA/NIDA NIH HHS/United States
- U01 DA041134/DA/NIDA NIH HHS/United States
- U01 DA041022/DA/NIDA NIH HHS/United States
- U01 DA041156/DA/NIDA NIH HHS/United States
- T32 AA013525/AA/NIAAA NIH HHS/United States
- U01 DA041089/DA/NIDA NIH HHS/United States
- F31 AA027118/AA/NIAAA NIH HHS/United States
- F31 DA040376/DA/NIDA NIH HHS/United States
- U01 DA041106/DA/NIDA NIH HHS/United States
- U01 DA041028/DA/NIDA NIH HHS/United States
- U01 DA041048/DA/NIDA NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
