Confinement-induced self-organization in growing bacterial colonies

Abstract

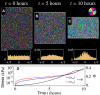
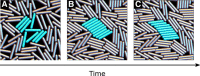
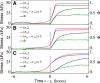
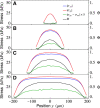
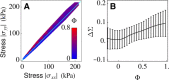
We investigate the emergence of global alignment in colonies of dividing rod-shaped cells under confinement. Using molecular dynamics simulations and continuous modeling, we demonstrate that geometrical anisotropies in the confining environment give rise to an imbalance in the normal stresses, which, in turn, drives a collective rearrangement of the cells. This behavior crucially relies on the colony's solid-like mechanical response at short time scales and can be recovered within the framework of active hydrodynamics upon modeling bacterial colonies as growing viscoelastic gels characterized by Maxwell-like stress relaxation.

Fig. 1. Colonization under confinement.

Snapshots of growing colonies at different time points. The boundary conditions are (A to F) rigid-wall confinement, (G to L) periodic confinement, and (M to R) no confinement in the y direction. Cells are color-coded by their orientation, as indicated by the color wheel in (A). In all three colonies, L_x = 70 μm, while L_y = 50 μm in (A) to (L). The colony height in (R) is about 300 μm. In all three scenarios, the direction of the confining channel is orthogonal to the red outlets, hence horizontal.

Fig. 2. Dynamics of the shrinking colony.

(A to C) Snapshots at different time points. Cells are color-coded by their orientations according to the color wheel in (C). The insets show the histograms of cell orientation at the corresponding time points. (D) Average stresses and the alignment parameter Φ as functions of time. The system contains 5000 cells in total, with a width L_x = 150 μm and an initial height L_y = 200 μm. The shrinking speed, i.e., the relative speed between the top and the bottom boundaries, is V_y = 10 μm/hour.

Fig. 3. Alignment mechanism in uniformly shrunk colonies.

(A) The cells in the central part of the panel are initially loosely packed and do not exhibit a preferential orientation. (B) As time progresses, the shrinkage causes them to form a stack of nine tightly packed cells roughly oriented at 45° with respect to the horizontal direction. (C) Last, as σ_yy > σ_xx, this cluster undergoes a collective rearrangement, whose effect is to redistribute the stress among the normal components by reorienting the cells along the horizontal direction. Snapshots correspond to different times in the simulations of a shrunk colony.

Fig. 4. Stress dynamics in growing colonies.

Normal stresses and the alignment parameter in region ℛ₀ of the colonies. The boundary conditions are (A) hard-wall confinement (see, e.g., Fig. 1, A to F), (B) periodic confinement (Fig. 1, G to L), and (C) no confinement (Fig. 1, M to R). In (A) and (B), the black dashed line indicates t_c, the time at which the colonies reach the horizontal boundary. In (C), t_c is set as the time where the normal stress difference in region ℛ₀ becomes nonzero. The results at each boundary condition are obtained by averaging over 200 simulations of growing colonies.

Fig. 5. Stress distribution in growing colonies.

Spatial distribution of stresses and alignment parameter Φ in a 20-μm-width region located at the center of the colony and spanning its entire height at different times. All the quantities are measured upon dividing the region into smaller boxes of height 10 μm and calculating their averages within each box. The channel is L_x = 70 μm wide, whereas the colony’s height is (A) 70 μm, (B) 150 μm, (C) 250 μm, and (D) 390 μm. The results are obtained by averaging over 100 simulations of growing colonies.

Fig. 6. Stress anisotropy in growing colonies.

Relation between the stresses and the alignment parameter in colonies unconfined in the y direction. (A) Two-dimensional map of the anisotropy parameter Φ as a function of the normal stresses σ_xx and σ_yy in channels of increasing width, in the range L_x = 50 to 150 μm with ΔL_x = 10 μm. The cyan line corresponds to the bisectrix ∣σ_xx∣ = ∣σ_yy∣. The maxima of Φ correspond to the maxima of ΔΣ for a given L_x value, and their periodicity results solely from the combination of multiple L_x values, each associated with a maximum in Φ and ΔΣ. (B) Stress anisotropy parameter, Eq. 3, versus the alignment parameter. The error bars show the SDs of data samples about the average values.

Fig. 7. Continuum model.

(A) Schematic representation of a one-dimensional active Maxwell material. Activity is incorporated into the constitutive equation in the form of a generator supplying a constant stress σ^a. (B) Steady-state configurations of nematic tensor Q for κ > 0. After an initial transient, the colony relaxes toward a state characterized by perfect longitudinal alignment. (C) Steady-state configuration of the density (black), v_x (blue), and v_y (red) in a colony with κ > 0. (D) Stress anisotropy parameter ΔΣ, Eq. 3, versus the alignment parameter Φ for a colony with κ > 0, compare with Fig. 6B. (E) Steady-state configurations of Q_xx (or Φ/2), Q_yy, and the stress anisotropy versus κ. As κ changes in sign from positive to negative, the colony switches from longitudinal to transverse orientation. The results are obtained from a numerical integration of Eqs. 8A to 8C on a rectangular domain with adsorbing boundaries in the x direction and periodic boundaries in the y direction.

Fig. 8. Bacteria alignment in merging colonies.

Experimental snapshots of the merger of three Vibrio cholerae colonies at different times. In the merging regions, marked with colored boxes, cells collectively align with the common tangent at the colonies’ front. Courtesy of A. Sengupta.