The length of the receiver operating characteristic curve and the two cutoff Youden index within a robust framework for discovery, evaluation, and cutoff estimation in biomarker studies involving improper receiver operating characteristic curves
- PMID: 33530129
- PMCID: PMC9976806
- DOI: 10.1002/sim.8869
The length of the receiver operating characteristic curve and the two cutoff Youden index within a robust framework for discovery, evaluation, and cutoff estimation in biomarker studies involving improper receiver operating characteristic curves
Abstract
During the early stage of biomarker discovery, high throughput technologies allow for simultaneous input of thousands of biomarkers that attempt to discriminate between healthy and diseased subjects. In such cases, proper ranking of biomarkers is highly important. Common measures, such as the area under the receiver operating characteristic (ROC) curve (AUC), as well as affordable sensitivity and specificity levels, are often taken into consideration. Strictly speaking, such measures are appropriate under a stochastic ordering assumption, which implies, without loss of generality, that higher measurements are more indicative for the disease. Such an assumption is not always plausible and may lead to rejection of extremely useful biomarkers at this early discovery stage. We explore the length of a smooth ROC curve as a measure for biomarker ranking, which is not subject to directionality. We show that the length corresponds to a divergence, is identical to the corresponding length of the optimal (likelihood ratio) ROC curve, and is an appropriate measure for ranking biomarkers. We explore the relationship between the length measure and the AUC of the optimal ROC curve. We then provide a complete framework for the evaluation of a biomarker in terms of sensitivity and specificity through a proposed ROC analogue for use in improper settings. In the absence of any clinical insight regarding the appropriate cutoffs, we estimate the sensitivity and specificity under a two-cutoff extension of the Youden index and we further take into account the implied costs. We apply our approaches on two biomarker studies that relate to pancreatic and esophageal cancer.
Keywords: divergence; Youden; isoperimetric; kernels; likelihood ratio; optimal ROC; sensitivity; specificity; stochastic ordering; two-cutoff ROC.
© 2021 John Wiley & Sons, Ltd.
Figures



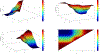
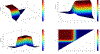
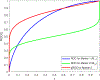

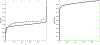
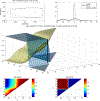
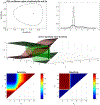
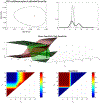
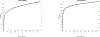
Similar articles
-
Construction of confidence intervals for the maximum of the Youden index and the corresponding cutoff point of a continuous biomarker.Biom J. 2019 Jan;61(1):138-156. doi: 10.1002/bimj.201700107. Epub 2018 Nov 8. Biom J. 2019. PMID: 30408224
-
Interrelationships Among Sensitivity, Precision, Accuracy, Specificity and Predictive Values in Bioassays, Represented as Combined ROC Curves with Integrated Cutoff Distribution Curves and Novel Index Values.Diagnostics (Basel). 2025 Feb 7;15(4):410. doi: 10.3390/diagnostics15040410. Diagnostics (Basel). 2025. PMID: 40002560 Free PMC article.
-
Statistical inference for the two-sample problem under likelihood ratio ordering, with application to the ROC curve estimation.Stat Med. 2023 Sep 10;42(20):3649-3664. doi: 10.1002/sim.9823. Epub 2023 Jun 13. Stat Med. 2023. PMID: 37311560
-
Receiver Operating Characteristic (ROC) Curves: The Basics and Beyond.Hosp Pediatr. 2024 Jul 1;14(7):e330-e334. doi: 10.1542/hpeds.2023-007462. Hosp Pediatr. 2024. PMID: 38932727 Review.
-
Understanding diagnostic tests 3: Receiver operating characteristic curves.Acta Paediatr. 2007 May;96(5):644-7. doi: 10.1111/j.1651-2227.2006.00178.x. Epub 2007 Mar 21. Acta Paediatr. 2007. PMID: 17376185 Review.
Cited by
-
Lineage specific extracellular vesicle-associated protein biomarkers for the early detection of high grade serous ovarian cancer.Sci Rep. 2023 Oct 26;13(1):18341. doi: 10.1038/s41598-023-44050-5. Sci Rep. 2023. PMID: 37884576 Free PMC article.
-
Biomarkers From Discovery to Clinical Application: In Silico Pre-Clinical Validation Approach in the Face of Lung Cancer.Biomark Insights. 2024 Oct 3;19:11772719241287400. doi: 10.1177/11772719241287400. eCollection 2024. Biomark Insights. 2024. PMID: 39371614 Free PMC article.
-
Combining multiple biomarkers linearly to minimize the Euclidean distance of the closest point on the receiver operating characteristic surface to the perfection corner in trichotomous settings.Stat Methods Med Res. 2024 Apr;33(4):647-668. doi: 10.1177/09622802241233768. Epub 2024 Mar 6. Stat Methods Med Res. 2024. PMID: 38445348 Free PMC article.
-
The diagnostic likelihood ratio function and modified test for trend: Identifying, evaluating, and validating nontraditional biomarkers in case-control studies.Stat Med. 2023 Dec 20;42(29):5313-5337. doi: 10.1002/sim.9912. Epub 2023 Sep 21. Stat Med. 2023. PMID: 37735925 Free PMC article.
-
The clinical meaning of the area under a receiver operating characteristic curve for the evaluation of the performance of disease markers.Epidemiol Health. 2022;44:e2022088. doi: 10.4178/epih.e2022088. Epub 2022 Oct 17. Epidemiol Health. 2022. PMID: 36265519 Free PMC article.
References
-
- Pepe MS (2003). The Statistical Evaluation of Medical Diagnostic Tests for Classification and Prediction. Oxford: Oxford University Press.
-
- Mann HB, Whitney DR (1947). On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Annals of Mathematical Statistics. 18(1): 50–60.
-
- Siegel RL, Miller KD, Jemal A. (2017) Cancer Statistics. CA: A Cancer Journal for Clinicians 67(1): 7–30. - PubMed
-
- Partensky C. (2013). Toward a better understanding of pancreatic ductal adenocarcinoma: glimmers of hope? (2013) Pancreas 42(5): 729–739. - PubMed
-
- Bamber D. (1975). The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. Journal of Mathematical Psychology 12(4): 387–415.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
