Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Feb 25;125(7):1861-1873.
doi: 10.1021/acs.jpcb.0c10329. Epub 2021 Feb 4.

Analytical 2-Dimensional Model of Nonpolar and Ionic Solvation in Water

Ajeet Kumar Yadav  1 , Pradipta Bandyopadhyay  1 , Tomaz Urbic  2 , Ken A Dill  3   4   5
Affiliations

Analytical 2-Dimensional Model of Nonpolar and Ionic Solvation in Water

Ajeet Kumar Yadav et al. J Phys Chem B. .

Abstract

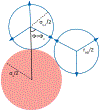
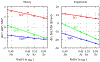
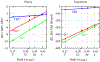
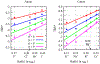
A goal in computational chemistry is computing hydration free energies of nonpolar and charged solutes accurately, but with much greater computational speeds than in today's explicit-water simulations. Here, we take one step in that direction: a simple model of solvating waters that is analytical and thus essentially instantaneous to compute. Each water molecule is a 2-dimensional dipolar hydrogen-bonding disk that interacts around small circular solutes with different nonpolar and charge interactions. The model gives good qualitative agreement with experiments. As a function of the solute radius, it gives the solvation free energy, enthalpy and entropy as a function of temperature for the inert gas series Ne, Ar, Kr, and Xe. For anions and cations, it captures relatively well the trends versus ion radius. This approach should be readily generalizable to three dimensions.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing financial interest.

Figures

Figure 1.
Figure 1.
Different interaction states of the water model: (1) HB state, (2) LJ state, (3) open state, and (4) solid state.
Figure 2.
Figure 2.
Definition of the critical angle ϕc. The shaded circle is the solute; other circles are water.
Figure 3.
Figure 3.
Top Panel: Approach of (1) anion and (2) cation to a water in the ionic model. Water dipole is also shown. Bottom Panel: Range of integration limits (see eq 11) a and b are shown.
Figure 4.
Figure 4.
Hydration free energies of the inert gases, vs temperature, for the different types of gas atoms, which have different radii. The unit of results from the theory is in reduced unit (see text).
Figure 5.
Figure 5.
Hydration enthalpies of the inert gases, vs temperature, for the different types of gas atoms, which have different radii. The unit of results from the theory is in reduced unit (see text).
Figure 6.
Figure 6.
Hydration entropies multiplied by temperature of the inert gases, vs temperature, for the different types of gas atoms, which have different radii. The unit of results from the theory is in reduced unit (see text).
Figure 7.
Figure 7.
Nonpolar hydration vs solute radius, from theory and experiments at a fixed temperature, for theory at 0.17 in reduced units and for the experiment at 25 °C.
Figure 8.
Figure 8.
Anion hydration as a function of solute radii. Theoretical results are shown in reduced units (T* = 0.15). Experiments are at 25 °C.
Figure 9.
Figure 9.
Cation hydration as a function of solute radii. Theoretical results are shown in reduced units (T* = 0.15). Experiments are at 25 °C.
Figure 10.
Figure 10.
Effect of varying the parameter γ on the ion hydration free energy as a function of solute radii.
Figure 11.
Figure 11.
Effect of varying the parameter γ on the ion hydration enthalpy as a function of solute radii.
Figure 12.
Figure 12.
Effect of varying the parameter γ on the ion hydration entropy as a function of solute radii.
Figure 13.
Figure 13.
Effect of varying the parameter δ on the ion hydration free energy as a function of solute radii.
Figure 14.
Figure 14.
Effect of varying the parameter δ on the ion hydration enthalpy as a function of solute radii.
Figure 15.
Figure 15.
Effect of varying the parameter δ on the ion hydration entropy as a function of solute radii.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

  • Crustwater: Modeling Hydrophobic Solvation.
    Yadav AK, Bandyopadhyay P, Coutsias EA, Dill KA. Yadav AK, et al. J Phys Chem B. 2022 Aug 18;126(32):6052-6062. doi: 10.1021/acs.jpcb.2c02695. Epub 2022 Aug 4. J Phys Chem B. 2022. PMID: 35926838 Free PMC article.

References

    1. Brini E; Fennell CJ; Fernandez-Serra M; Hribar-Lee B; Lukšič M; Dill KA How Water’s Properties Are Encoded in Its Molecular Structure and Energies. Chem. Rev 2017, 117, 12385–12414. - PMC - PubMed
    1. Hermann RB Theory of Hydrophobic Bonding. II. The Correlation of Hydrocarbon Solubility in Water with Solvent Cavity Surface Area. J. Phys. Chem 1972, 76, 2754–2759.
    1. Urbič T; Vlachy V; Kalyuzhnyi YV; Southall NT; Dill KA A Two-Dimensional Model of Water: Solvation of Nonpolar Solutes. J. Chem. Phys 2002, 116, 723–729.
    1. Urbič T; Vlachy V; Kalyuzhnyi YV; Dill KA Orientation-Dependent Integral Equation Theory for a Two-Dimensional Model of Water. J. Chem. Phys 2003, 118, 5516–5525.
    1. Urbic T; Vlachy V; Kalyuzhnyi YV; Dill KA Theory for the Solvation of Nonpolar Solutes in Water. J. Chem. Phys 2007, 127, 174505. - PubMed

Publication types