Nonhuman Primates Satisfy Utility Maximization in Compliance with the Continuity Axiom of Expected Utility Theory

Abstract

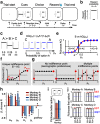
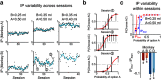
Expected Utility Theory (EUT), the first axiomatic theory of risky choice, describes choices as a utility maximization process: decision makers assign a subjective value (utility) to each choice option and choose the one with the highest utility. The continuity axiom, central to Expected Utility Theory and its modifications, is a necessary and sufficient condition for the definition of numerical utilities. The axiom requires decision makers to be indifferent between a gamble and a specific probabilistic combination of a more preferred and a less preferred gamble. While previous studies demonstrated that monkeys choose according to combinations of objective reward magnitude and probability, a concept-driven experimental approach for assessing the axiomatically defined conditions for maximizing utility by animals is missing. We experimentally tested the continuity axiom for a broad class of gamble types in 4 male rhesus macaque monkeys, showing that their choice behavior complied with the existence of a numerical utility measure as defined by the economic theory. We used the numerical quantity specified in the continuity axiom to characterize subjective preferences in a magnitude-probability space. This mapping highlighted a trade-off relation between reward magnitudes and probabilities, compatible with the existence of a utility function underlying subjective value computation. These results support the existence of a numerical utility function able to describe choices, allowing for the investigation of the neuronal substrates responsible for coding such rigorously defined quantity.SIGNIFICANCE STATEMENT A common assumption of several economic choice theories is that decisions result from the comparison of subjectively assigned values (utilities). This study demonstrated the compliance of monkey behavior with the continuity axiom of Expected Utility Theory, implying a subjective magnitude-probability trade-off relation, which supports the existence of numerical utility directly linked to the theoretical economic framework. We determined a numerical utility measure able to describe choices, which can serve as a correlate for the neuronal activity in the quest for brain structures and mechanisms guiding decisions.

Keywords: continuity axiom; decision making; expected utility theory; reward risk; utility.

Figure 1.

Experimental design and consistency of choice behavior. a, Trial sequence. Monkeys chose between two options by moving a cursor (gray dot) with a joystick to one side of the screen. After a delay, the reward corresponding to the selected cue was delivered. b, Visual cues indicated magnitude and probability of possible outcomes through horizontal bars' vertical position and width, respectively. c-e, Continuity axiom test. The continuity axiom was tested through choices between a fixed gamble B and a probabilistic combination of A and C (AC). A, B, and C were ordered reward magnitudes (c); AC was a gamble between A and C, with probabilities p_A and 1 – p_A, respectively (d); different shades of blue represent different p_A values (darker for higher p_A). The continuity axiom implies the existence of a unique AC combination (p_A = α) corresponding to choice indifference between the two options (B ∼ AC, vertical line in e), with the existence of a p_A for which B ≻ AC and of a different p_A for which AC ≻ B (vertical dashed lines). The value of α was identified by fitting a softmax function (Eq. 2, red line) to the proportion of AC choices (blue dots). f, g, Compliance and violation. Choice pattern compatible with the continuity axiom (f) and possible axiom violations (g). Red dots represent the proportion of AC choices when p_A = 0 or 1, corresponding to the axiom's initial requirement (A ≻ B and B ≻ C, implying P(A ≻ B) > 0.5 and P(C ≻ B) < 0.5). h-j, Consistency of choice behavior. The standardized β coefficients from logistic regressions of single trials' behavior (h) showed that the main choice-driving variables were reward magnitude (m_R, m_L) and probability (p_R, p_L) for all animals, both for left (L) and right (R) choices; previous trial's chosen side (preCh_R) and reward (preRew_R) did not consistently explain animals' choices (error bars indicate 95% CI across sessions). *p < 0.05 (one-sample t test, FDR-corrected). No. of sessions per animal: 100 (A), 81 (B), 24 (C), 15 (D). In choices between options with different probability of delivering the same reward magnitude, the better option was preferred on average by all animals, demonstrating compliance with FSD (i) (error bars indicate binomial 95% CI; no. of tests per animal: 28 (A), 24 (B), 15 (C), 23 (D); average no. of trials per test: 12 (A), 13 (B), 11 (C), 34 (D)). In choices between sure rewards (bars represent average across all sessions; gray dots represent single sessions; error bars indicate binomial 95% CI) animals preferred A to B, B to C, and A to C (j), complying with both WST and SST (WST: proportion of choices of the better option >0.5 (blue dashed line); SST: proportion of A over C choices (red line) ≥ other choice proportions).

Figure 2.

Experimental test of the continuity axiom. a-c, Compliance with the continuity axiom. The axiom was tested through choices between a gamble B and a varying AC-combined gamble (left, visual stimuli for an example choice pair with p_A = 0.5 (a,b) or p_A = 0.375 (c)); increasing p_A values resulted in gradually increasing preferences for the AC option. In each plot: Gray dots represent the proportion of AC choices in single sessions. Black circles represent the proportions across all tested sessions. Vertical bars represent the binomial 95% CIs. Filled circles represent significant difference from 0.5 (binomial test, p < 0.05). The tests were repeated using different A and B values (b) as well as non-zero C values in a modified task (c). All 4 animals complied with the continuity axiom by showing increasing preferences for increasing probability of gamble A (rank correlation, p < 0.05), with the AC option switching from nonpreferred (P(choose AC) < 0.5) to preferred (P(choose AC) > 0.5) (binomial test, p < 0.05). Each IP (α, vertical line) was computed as the p_A for which a data-fitted softmax function (Eq. 2) had a value of 0.5 (horizontal bars represent 95% CI); α values shifted coherently with changes in A and B values in all 4 animals, indicating a continuous MP trade-off relation. For single sessions' IP values, see Figure 3.

Figure 3.

Variability of IP across and within sessions. a, Evolution of the IP as a function of session number (blue curve indicates 5-session moving average), for the three continuity axiom tests presented in Figure 2a, b (Monkeys A, B). b, Choice proportion for the AC gamble in three example sessions (as indicated in a). Vertical bars represent binomial 95% CI, indicating a significant preference (black dot) when not crossing the horizontal dashed line. c, Top, Preferences in the first half (blue) and in the second half (red) of a session (one example session, Monkey B). Bottom, Average IP change across all sessions. Error bars indicate SE. *p < 0.05, IP difference significantly different from zero (t test).

Figure 4.

ICs in the MP space. a, Representation of the continuity axiom test in the MP space. The gambles used for testing the axiom can be mapped into the MP diagram. Preference in choices between B (circle) and combinations of A and C (graded blue dots) is represented by an arrow pointing in the direction of the preferred option (bottom), consistently with the proportion of choices for the AC option (top). Each continuity axiom test resulted in an IP (vertical line, top), represented as a black dot in the MP space (bottom). b, IC. IPs (gray dot indicates single session; black dot indicates average across sessions; error bar indicates SE) obtained using different A values (step 0.01 ml) shifted continuously, producing an IC in the MP space (area: 95% CI). Curve indicates best fitting power function. Data from Monkey A (5 sessions, 1781 trials). c, d, Indifference map. ICs for different B values (colored thick curves) described the gradual variation of the average IPs (colored dots, with SE bars) for each B. ICs were modeled as power functions (for comparison with hyperbolic and linear fits, see Extended Data Figure 4-1). Small dots indicate IPs measured in single sessions. Both sure rewards (c) and probabilistic gambles (d) as B options, produced coherent indifference maps, with smooth and nonoverlapping ICs. Dashed curves indicate points with the same objective EV, highlighting the subjective quality of ICs.

Figure 5.

Theoretical relation between utility function and indifference map. Sample indifference maps obtained from different utility functions, with a representing the single parameter of a power function ($U\left(m\right)={\left(m/m_0\right)}^a$, with $m_0=0.5ml$). The IC for a degenerate gamble B was analytically obtained as a function of magnitude values, from the equation ${EU}_B=U\left(m\right)·p$. By solving the equation for p, the IC equation can be obtained as follows: $p\left(m\right)={\left(m_B/m\right)}^a$, where $m_B$ is the magnitude of a degenerate gamble B. The three utility shapes are directly related to different risk attitudes: risk neutrality for linear utility (a), risk seeking for convex utility (b), and risk aversion for concave utility (c). In all plots, gray curves indicate risk neutrality (i.e., choices based on the objective EV of gambles). The indifference map globally warps according to the risk attitude.

Figure 6.

ICs are compatible with economic models. a, Utility functions. Single sessions' utility functions (gray) and averages (black) estimated through MLE using single-trial choice data. The two estimated parameters (a and b in inset, histograms of log values) were both significantly positive, indicating S-shaped utility functions. b, EUT-predicted ICs. Indifference map reconstructed using the estimated utility functions. Light-colored curves indicate the measured indifference map (see Fig. 4c). Red horizontal lines indicate the distance between measured and modeled IPs. Dashed gray curves indicate points with equal EV, corresponding to a linear utility model. For the theoretical relation between the utility function and the ICs, see Figure 5. c, Comparison of modeled and revealed preferences. Percentage of choices for the AC gamble (P(AC)) measured (black) and modeled using three models (red), for three example A-B-C triplets (top, A and B in ml, C = 0 ml). The EV model could only predict IPs equal to the EVs (gray vertical lines), with a larger error in the prediction of the P(AC) (vertical dotted red lines) compared with the EU model. The PW model, which included a subjective PW, was better at capturing the revealed preferences only in specific cases (e.g., B = 0.15, A = 0.25 in Monkey B).

Figure 7.

Comparison of economic models. Recovered utility function, PW function, and corresponding indifference map for each economic model (rows). Gray curves indicate single-session estimates. Black curves indicate the corresponding means, plotted by averaging the recovered parameters across all sessions. Red lines indicate linear utility and PW functions, for comparison. The EV, EU, and additive models assume linear PW. The mean-variance model (EV-Risk) does not have a utility representation. Other conventions and symbols are as in Figure 6b.

Figure 8.

Three-dimensional utility representation. a, Indifference map resulting from the best-fitting PW model. Black curves indicate the iso-utility points (i.e., the ICs) for 9 equally spaced EV levels (0.05-0.45 ml, step: 0.05 ml). Colors (blue to red) represent utility values (from 0 to 1). b, Three-dimensional representation of utility values, highlighting the continuous relation between objective quantities (m, p) and subjective values (utility): for any two-outcome gamble, corresponding to a {m, p} pair, a utility level can be mathematically computed using the two-dimensional function defined by the best-fitting PW model (V(m,p) = U(m) · w(p)). This relation can be used to identify utility-coding neurons: the activity of a neuron coding utility should follow the three-dimensional surface across the whole tested region of the MP space.

Figure 9.

Continuity axiom test in the Marschak-Machina triangle. a, Three-outcome gambles. Gambles with three fixed outcome magnitudes and any combination of outcome probabilities can be represented in the Marschak-Machina triangle. The visual cue (inset) for three-outcome gambles included three horizonal lines indicating the three possible outcome magnitudes (vertical position) and the respective probabilities p₁, p₂, and p₃ (line width). b, Scheme of the continuity axiom test. Three-outcome gambles used to test the axiom (top) can be represented in the Marschak-Machina triangle (bottom right) together with the B gamble (circle) and the resulting IP (red dot). Arrows point toward the preferred option, consistently with the proportion of AC choices (bottom left). c, Continuity axiom test in the Marschak-Machina triangle. Average IPs (black dots) and from single sessions (red dots) were consistently elicited, indicating compliance with the continuity axiom in choices between two- and three-outcome gambles. d, Revealed preferences in choices between two- and three-outcome gambles. Average measured percentage of AC choices as a function of the probability of obtaining the A option (graded blue dots). Each average IP (black vertical line) corresponds to a black dot in c. Other symbols are as in Figure 3.